题目内容
如图所示，两木块的质量分别为m1和m2，两轻质弹簧的劲度系数分别为k1和k2，整个系统处于平衡状态（弹簧k2与地面不拴接，其它接触处均为栓接），现缓慢的向上提上面的木块m1，只到下面的弹簧刚好离开地面，求在这个过程中两木块移动的距离分别为多少？
解：对m1与m2整体分析，在初始状态 （m1+m2）g=k2x2
故m2上升的距离为
；
初始状态的m1 k1x1=m1g，故
；
末状态时的m2
，故
；
所以m1上升的距离为：h=x1+x1′+x2=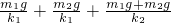
=（m1+m2）g（
）
答：这个过程中下方的木块上升的距离为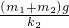
；上方的木块上升的距离为（m1+m2）g（）．
分析：开始时两个弹簧均处于压缩状态，根据胡克定律求解出两个弹簧的压缩量；下面的弹簧刚好离开地面时，下方弹簧恢复原长，上方的弹簧被拉长，根据胡克定律求解出拉伸量；最后结合空间关系得到两木块移动的距离．
点评：本题关键是根据胡克定律求解出弹簧的压缩量和伸长量，基础题．
故m2上升的距离为
；初始状态的m1 k1x1=m1g，故
；末状态时的m2
，故；所以m1上升的距离为：h=x1+x1′+x2=
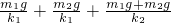=（m1+m2）g（）答：这个过程中下方的木块上升的距离为
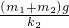；上方的木块上升的距离为（m1+m2）g（）．分析：开始时两个弹簧均处于压缩状态，根据胡克定律求解出两个弹簧的压缩量；下面的弹簧刚好离开地面时，下方弹簧恢复原长，上方的弹簧被拉长，根据胡克定律求解出拉伸量；最后结合空间关系得到两木块移动的距离．
点评：本题关键是根据胡克定律求解出弹簧的压缩量和伸长量，基础题．
练习册系列答案
相关题目
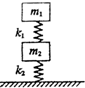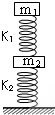如图所示，两木块的质量分别为m1和m2，两轻质弹簧的劲度系数分别为k1和k2，上面木块压在上面的弹簧上（但不栓接），整个系统处于平衡状态，现缓慢向上提上面的木块，直到它刚离开上面弹簧，求在这过程中下面木块移动的距离．
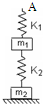如图所示，两木块的质量分别为m1和m2，两轻质弹簧的劲度系数分别为k1和k2，两弹簧与两木块均连接在一起，整个系统处于平衡状态．现缓慢向上提上面弹簧的上端A，直到下面的木块m2刚离开地面．在此过程中上面弹簧的上端A移动的距离为（ ）
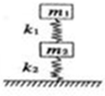如图所示，两木块的质量分别为m1和m2，两轻质弹簧的劲度系数分别为k1和k2，整个系统处于平衡状态，则k1，k2两轻质弹簧的形变量大小分别为（ ）
如图所示，两木块的质量分别为m1和m2，两轻质弹簧的度系数分别为k1的k2，上面木块压在上面的弹簧上（但不拴接），整个系统处于平衡状态．现缓慢向上提上面的木块，直到它刚离开上面弹簧．在这个过程中两木块m1和m2移动的距离为（ ）A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
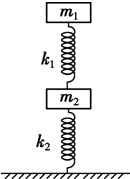如图所示，两木块的质量分别为m1和m2，两轻质弹簧的劲度系数分别为k1和k2，上面的木块压在上面的弹簧上（但不拴接），整个系统处于平衡状态．现缓慢地向上提上面的木块，直到它刚离开上面的弹簧，求：