题目内容
如图所示，两木块的质量分别为m1和m2，两轻质弹簧的劲度系数分别为k1和k2，两弹簧与两木块均连接在一起，整个系统处于平衡状态．现缓慢向上提上面弹簧的上端A，直到下面的木块m2刚离开地面．在此过程中上面弹簧的上端A移动的距离为（ ）分析：开始时上面弹簧处于原长状态，下面弹簧处于压缩状态；缓慢向上提上面弹簧的上端A，直到下面的木块刚离开地面，此时上下两个弹簧均处于拉伸状态；根据胡克定律求解出各个行变量，然后结合几何关系求解上面弹簧的上端A移动的距离．
解答：解：开始时上面弹簧处于原长状态，下面弹簧处于压缩状态，压缩量为：x1=
；
缓慢向上提上面弹簧的上端A，直到下面的木块刚离开地面，此时上下两个弹簧均处于拉伸状态，上面弹簧拉伸量为：x2=
；下面弹簧的拉伸量为：x3=
；
故A点的上移量为：△x=x1+x2+x3=
+
；
故选C．
| m1g |
| k2 |
缓慢向上提上面弹簧的上端A，直到下面的木块刚离开地面，此时上下两个弹簧均处于拉伸状态，上面弹簧拉伸量为：x2=
| m1g+m2g |
| k1 |
| m2g |
| k2 |
故A点的上移量为：△x=x1+x2+x3=
| (m1+m2)g |
| k1 |
| (m1+m2)g |
| k2 |
故选C．
点评：本题关键是根据胡克定律求解弹簧初始时刻和末时刻的形变情况，然后结合几何关系确定A点的移动距离．
练习册系列答案
相关题目
如图所示，两木块的质量分别为m1和m2，两轻质弹簧的劲度系数分别为k1和k2，上面木块压在上面的弹簧上（但不栓接），整个系统处于平衡状态，现缓慢向上提上面的木块，直到它刚离开上面弹簧，求在这过程中下面木块移动的距离．
如图所示，两木块的质量分别为m1和m2，两轻质弹簧的劲度系数分别为k1和k2，整个系统处于平衡状态，则k1，k2两轻质弹簧的形变量大小分别为（ ）
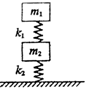如图所示，两木块的质量分别为m1和m2，两轻质弹簧的度系数分别为k1的k2，上面木块压在上面的弹簧上（但不拴接），整个系统处于平衡状态．现缓慢向上提上面的木块，直到它刚离开上面弹簧．在这个过程中两木块m1和m2移动的距离为（ ）A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
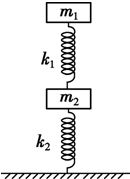如图所示，两木块的质量分别为m1和m2，两轻质弹簧的劲度系数分别为k1和k2，上面的木块压在上面的弹簧上（但不拴接），整个系统处于平衡状态．现缓慢地向上提上面的木块，直到它刚离开上面的弹簧，求：