题目内容
6.从某一高度先后由静止释放两个相同的小球甲和乙,若两球被释放的时间间隔为1s从某一高度先后由静止释放两个相同的小球甲和乙,若两球被释放的时间间隔为1s,在不计空气阻力的情况下,它们在空中的运动过程中( )| A. | 甲、乙两球的距离越来越大,甲、乙两球的速度之差越来越大 | |
| B. | 在相等的时间内甲、乙两球速度的变化量不相等 | |
| C. | 甲、乙两球的距离越来越大,甲、乙两球的速度之差保持不变 | |
| D. | 甲、乙两球的距离始终保持不变,甲、乙两球的速度之差保持不变 |
分析 甲乙两球均做自由落体运动,由位移公式列出它们的距离与时间关系的表达式,再求出速度之差与时间的关系.
解答 解:A、C、D、设乙运动的时间为t,则甲运动时间为t+1,
则两球的距离x=$\frac{1}{2}{g(t+1)}^{2}$-$\frac{1}{2}{gt}^{2}$=gt+$\frac{1}{2}g$,可见,两球间的距离随时间推移,越来越大.
两球速度之差为:△v=g(t+1)-gt=g,所以甲乙两球速度之差保持不变.
所以C正确,AD错误.
B、在相等的时间内甲、乙两球速度的变化量△v′=g△t,由于加速度相等,所以是相等的.故B错误.
故选:C
点评 本题是自由落体运动位移公式和速度公式的直接应用,难度不大,属于基础题.

练习册系列答案
相关题目
9.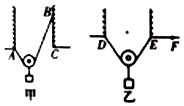 有甲、乙两根完全相同的轻绳,甲绳A、B两端按图甲的方式固定,然后将一挂有质量为M的重物的光滑轻质动滑轮挂于轻绳上,当滑轮静止后,设绳子的张力大小为T1;乙绳两端按图乙的方式连接,然后将同样的定滑轮且挂有质量为M的重物挂于乙轻绳上,当滑轮静止后,设乙绳子的张力大小为T2.现甲绳的B端缓慢向下移动至C点,乙绳的E端缓慢移动至F点,在两绳的移动过程中,下列说法正确的是( )
有甲、乙两根完全相同的轻绳,甲绳A、B两端按图甲的方式固定,然后将一挂有质量为M的重物的光滑轻质动滑轮挂于轻绳上,当滑轮静止后,设绳子的张力大小为T1;乙绳两端按图乙的方式连接,然后将同样的定滑轮且挂有质量为M的重物挂于乙轻绳上,当滑轮静止后,设乙绳子的张力大小为T2.现甲绳的B端缓慢向下移动至C点,乙绳的E端缓慢移动至F点,在两绳的移动过程中,下列说法正确的是( )
 有甲、乙两根完全相同的轻绳,甲绳A、B两端按图甲的方式固定,然后将一挂有质量为M的重物的光滑轻质动滑轮挂于轻绳上,当滑轮静止后,设绳子的张力大小为T1;乙绳两端按图乙的方式连接,然后将同样的定滑轮且挂有质量为M的重物挂于乙轻绳上,当滑轮静止后,设乙绳子的张力大小为T2.现甲绳的B端缓慢向下移动至C点,乙绳的E端缓慢移动至F点,在两绳的移动过程中,下列说法正确的是( )
有甲、乙两根完全相同的轻绳,甲绳A、B两端按图甲的方式固定,然后将一挂有质量为M的重物的光滑轻质动滑轮挂于轻绳上,当滑轮静止后,设绳子的张力大小为T1;乙绳两端按图乙的方式连接,然后将同样的定滑轮且挂有质量为M的重物挂于乙轻绳上,当滑轮静止后,设乙绳子的张力大小为T2.现甲绳的B端缓慢向下移动至C点,乙绳的E端缓慢移动至F点,在两绳的移动过程中,下列说法正确的是( )| A. | T1、T2都变大 | B. | T1变大、T2变小 | C. | T1、T2都不变 | D. | T1不变、T2变大 |
14.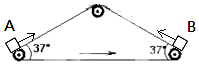 三角形传送带以1m/s的速度逆时针匀速转动,两边的传送带长都是2m且与水平方向的夹角均为37°.现有两个小物块A、B从传送带底端都以4m/s的初速度冲上传送带,物块与传送带间的动摩擦因数都是0.5,下列说法正确的是( )
三角形传送带以1m/s的速度逆时针匀速转动,两边的传送带长都是2m且与水平方向的夹角均为37°.现有两个小物块A、B从传送带底端都以4m/s的初速度冲上传送带,物块与传送带间的动摩擦因数都是0.5,下列说法正确的是( )
 三角形传送带以1m/s的速度逆时针匀速转动,两边的传送带长都是2m且与水平方向的夹角均为37°.现有两个小物块A、B从传送带底端都以4m/s的初速度冲上传送带,物块与传送带间的动摩擦因数都是0.5,下列说法正确的是( )
三角形传送带以1m/s的速度逆时针匀速转动,两边的传送带长都是2m且与水平方向的夹角均为37°.现有两个小物块A、B从传送带底端都以4m/s的初速度冲上传送带,物块与传送带间的动摩擦因数都是0.5,下列说法正确的是( )| A. | 物块A、B都能到达传送带顶端 | |
| B. | 两物块在传送带上运动的全过程中,物块A、B所受摩擦力一直阻碍物块A、B的运动 | |
| C. | 物块A上冲到与传送带速度相同的过程中,物块相对传送带运动的路程为1.2m | |
| D. | 物块B在上冲过程中在传送带上留下的划痕长度为0.45m |
1.一台电动机,额定电压是100V,电阻是1Ω,正常工作时,通过的电流为5A,则电动机的转动功率为( )
| A. | 500W | B. | 25W | C. | 2000W | D. | 475W |
11. 为了节省能量,某商场安装了智能化的电动扶梯.无人乘行时,扶梯运转得很慢;有人站上扶梯时,它会先慢慢加速,再匀速运转.一顾客乘扶梯上楼,恰好经历了这两个过程,如图所示.那么下列说法中正确的是( )
为了节省能量,某商场安装了智能化的电动扶梯.无人乘行时,扶梯运转得很慢;有人站上扶梯时,它会先慢慢加速,再匀速运转.一顾客乘扶梯上楼,恰好经历了这两个过程,如图所示.那么下列说法中正确的是( )
 为了节省能量,某商场安装了智能化的电动扶梯.无人乘行时,扶梯运转得很慢;有人站上扶梯时,它会先慢慢加速,再匀速运转.一顾客乘扶梯上楼,恰好经历了这两个过程,如图所示.那么下列说法中正确的是( )
为了节省能量,某商场安装了智能化的电动扶梯.无人乘行时,扶梯运转得很慢;有人站上扶梯时,它会先慢慢加速,再匀速运转.一顾客乘扶梯上楼,恰好经历了这两个过程,如图所示.那么下列说法中正确的是( )| A. | 扶梯对顾客作用力的方向始终是竖直向上 | |
| B. | 扶梯加速时,扶梯对顾客的摩擦力方向为水平向右 | |
| C. | 扶梯对顾客作用力的方向先指向右上方,再竖直向上 | |
| D. | 顾客先受到三个力的作用,后受到两个力的作用 |
15. 如图所示,物体P静止在倾角为α的斜面上,其所受的重力可分解成平行于斜面的F1和垂直于斜面的F2,则( )
如图所示,物体P静止在倾角为α的斜面上,其所受的重力可分解成平行于斜面的F1和垂直于斜面的F2,则( )
 如图所示,物体P静止在倾角为α的斜面上,其所受的重力可分解成平行于斜面的F1和垂直于斜面的F2,则( )
如图所示,物体P静止在倾角为α的斜面上,其所受的重力可分解成平行于斜面的F1和垂直于斜面的F2,则( )| A. | P受到重力、F1、F2、支持力和摩擦力的作用 | |
| B. | P受到重力、支持力和摩擦力的作用 | |
| C. | 当α增大时,F2也随着增大 | |
| D. | 当α减小时,F1却逐渐增大 |
 如图,在一端封闭、长约E的玻璃管内注满清水,水中放一个红蜡做的小圆柱体R.将玻璃管的开口端用橡胶塞塞紧.若仅将玻璃管倒置,蜡块R将沿玻璃管向上匀加速一小段距离后开始匀速上升.若将玻璃管倒置的同时,将玻璃管沿水平方向向右匀速移动.设竖直向上为y轴,水平向右为x轴,则红蜡块R的运动轨迹可能是以下四个图中( )
如图,在一端封闭、长约E的玻璃管内注满清水,水中放一个红蜡做的小圆柱体R.将玻璃管的开口端用橡胶塞塞紧.若仅将玻璃管倒置,蜡块R将沿玻璃管向上匀加速一小段距离后开始匀速上升.若将玻璃管倒置的同时,将玻璃管沿水平方向向右匀速移动.设竖直向上为y轴,水平向右为x轴,则红蜡块R的运动轨迹可能是以下四个图中( )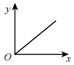
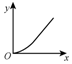


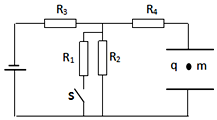 如图15所示,四个电阻阻值相等,即R1=R2=R3=R4=R,当电键S断开时,有一质量为m,带电量为q的小球恰能静止于水平放置的平行板电容器的中点.现闭合电键S,这个带电小球便向平行板电容器的一个极板运动,并和此板碰撞,碰撞过程中小球没有机械能损失,只是碰后小球所带电量发生变化,碰后小球带有和该板同种性质的电荷,并恰能运动到另一极板,设两极板间距离为d,电容器的电容为C,不计电源内阻,求:
如图15所示,四个电阻阻值相等,即R1=R2=R3=R4=R,当电键S断开时,有一质量为m,带电量为q的小球恰能静止于水平放置的平行板电容器的中点.现闭合电键S,这个带电小球便向平行板电容器的一个极板运动,并和此板碰撞,碰撞过程中小球没有机械能损失,只是碰后小球所带电量发生变化,碰后小球带有和该板同种性质的电荷,并恰能运动到另一极板,设两极板间距离为d,电容器的电容为C,不计电源内阻,求: