题目内容
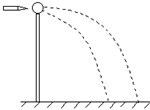把一质量为m=0.2kg的小球放在高度h=5.0m的直杆的顶端，如图所示，一颗质量m′=0.01kg的子弹以V0=500m/s的速度沿水平方向击中小球，并穿过球心，小球落地处离杆的距离S1=20m．求子弹落地处离杆的距离S2．分析：小球被击穿后做平抛运动，根据高度与水平距离求出子弹击穿小球后的速度．子弹击穿小球的过程，遵守动量守恒，根据动量守恒定律求出击穿后子弹的速度，再由平抛运动的规律求出子弹落地点距杆的水平距离S2．
解答：解：球被击中后做平抛运动，
平抛的时间为 t=
=
=1s
小球平抛的初速度为 V球=
=
s=20s，
由动量守恒定律得：m′V0=m′V0′+mV球
即 0.01×500=0.01×V0′+0.2×20，
子弹的速度为 V0′=100m/s
子弹落地处离杆的距离 S2=100×1=100m．
答：子弹落地处离杆的距离为100m．
平抛的时间为 t=
|
|
小球平抛的初速度为 V球=
| s1 |
| t |
| 20 |
| 1 |
由动量守恒定律得：m′V0=m′V0′+mV球
即 0.01×500=0.01×V0′+0.2×20，
子弹的速度为 V0′=100m/s
子弹落地处离杆的距离 S2=100×1=100m．
答：子弹落地处离杆的距离为100m．
点评：子弹射击物体过程，基本规律是动量守恒和能量守恒．本题是动量守恒与平抛运动的综合，常规题．
练习册系列答案
名校课堂系列答案
相关题目
（2004?青岛一模）把一个质量为 m=0.2 0kg的小球放在高度为 h=5.0m的直杆的顶端，如图所示，一颗质量为m′=0.01kg的子弹以速度 v0=500m/s沿水平方向击穿小球，小球落地点与杆的水平距离S=20m．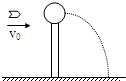
把一质量为M=0.2kg的小球放在高度h=5.0m的直杆的项端．一颗质量m=0.01kg的子弹以v0=500m/s的速度沿水平方向击中小球，并穿过球心，小球落地处离杆的距离s=20m．求：
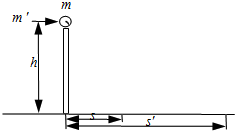
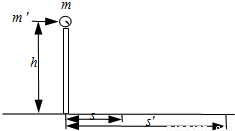把一个质量为 m=0.2 0kg的小球放在高度为 h=5.0m的直杆的顶端，如图所示，一颗质量为m′=0.01kg的子弹以速度 v=500m/s沿水平方向击穿小球，小球落地点与杆的水平距离S=20m．