题目内容
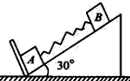 在倾角为30°的足够长的光滑斜面底端固定一个垂直于斜面的挡板,物体A,B用轻弹簧连接并放在斜面上,系统处于静止状态,如图所示,已知物体A的质量mA=2kg,物体B的质量mB=1kg,弹簧的劲度系数为k=100N/m,现在将物体B从静止状态沿斜面向下压10cm后释放,g取10m/s2,则在物体B运动的过程中
在倾角为30°的足够长的光滑斜面底端固定一个垂直于斜面的挡板,物体A,B用轻弹簧连接并放在斜面上,系统处于静止状态,如图所示,已知物体A的质量mA=2kg,物体B的质量mB=1kg,弹簧的劲度系数为k=100N/m,现在将物体B从静止状态沿斜面向下压10cm后释放,g取10m/s2,则在物体B运动的过程中
- A.物体A不会离开挡板,A对挡板的最小压力为5N
- B.物体A不会离开挡板,A对挡板的最小压力为10N
- C.物体A不会离开挡板,物体B振动的振幅为15cm
- D.物体A会离开挡板
A
分析:虽然在B运动的过程中物体A会不会运动不清楚,但我们可以假设A始终不动,求出弹簧的最大拉力Fm,然后将Fm与mAgsin30°进行比较来判断A会不会离开挡板.
解答:A、B的重力沿斜面的分力分别为GA=mAgsin30°=10N、GB =mBgsin30°=5N,弹簧的压缩量为:
x0=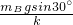 =5cm.
=5cm.
下压x=10cm时,释放瞬间B的合外力大小为k (x+x0)-GB=10N,方向沿斜面向上.
假设A始终不动,则释放后B将做简谐运动,振幅为10cm,根据对称性可知,B运动到最高点时的合外力大小亦为10N、方向沿斜面向下,这时弹簧的拉力达到最大,由F合=Fm+GB得,最大的拉力Fm=F合-GB=10N-5N=5N,由于Fm<GA,所以假设成立即A不会离开挡板,A对挡板的最小压力为GA -Fm=5N.故A正确,BCD错误;
故选A.
点评:因轻弹簧两端分别与两物体连接,其形变发生改变过程需要一段时间,即弹簧的弹力不发生突变,所以释放瞬间弹簧的弹力仍等于释放前的弹力.
注意:由于受到“水平方向上做简谐运动的弹簧振子的平衡位置处弹力为零”定势思维的影响,本题极易认为B振动的振幅为x+x0=15cm而错选C,即本题中应注意平衡位置是物体静止的位置.
分析:虽然在B运动的过程中物体A会不会运动不清楚,但我们可以假设A始终不动,求出弹簧的最大拉力Fm,然后将Fm与mAgsin30°进行比较来判断A会不会离开挡板.
解答:A、B的重力沿斜面的分力分别为GA=mAgsin30°=10N、GB =mBgsin30°=5N,弹簧的压缩量为:
x0=
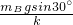 =5cm.
=5cm.下压x=10cm时,释放瞬间B的合外力大小为k (x+x0)-GB=10N,方向沿斜面向上.
假设A始终不动,则释放后B将做简谐运动,振幅为10cm,根据对称性可知,B运动到最高点时的合外力大小亦为10N、方向沿斜面向下,这时弹簧的拉力达到最大,由F合=Fm+GB得,最大的拉力Fm=F合-GB=10N-5N=5N,由于Fm<GA,所以假设成立即A不会离开挡板,A对挡板的最小压力为GA -Fm=5N.故A正确,BCD错误;
故选A.
点评:因轻弹簧两端分别与两物体连接,其形变发生改变过程需要一段时间,即弹簧的弹力不发生突变,所以释放瞬间弹簧的弹力仍等于释放前的弹力.
注意:由于受到“水平方向上做简谐运动的弹簧振子的平衡位置处弹力为零”定势思维的影响,本题极易认为B振动的振幅为x+x0=15cm而错选C,即本题中应注意平衡位置是物体静止的位置.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
 (2009?盐城一模)如图甲所示,在倾角为30°的足够长的光滑斜面上,有一质量为m的物体,受到沿斜面方向的力F作用,力F按图乙所示规律变化(图中纵坐标是F与mg的比值,力沿斜面向上为正).则物体运动的速度v随时间t变化的规律是下图中的(物体的初速度为零,重力加速度取10m/s2)( )
(2009?盐城一模)如图甲所示,在倾角为30°的足够长的光滑斜面上,有一质量为m的物体,受到沿斜面方向的力F作用,力F按图乙所示规律变化(图中纵坐标是F与mg的比值,力沿斜面向上为正).则物体运动的速度v随时间t变化的规律是下图中的(物体的初速度为零,重力加速度取10m/s2)( )

 在倾角为θ=30°的足够长的斜面底端,木块A以某一初速度v0沿斜面向上运动,若木块与斜面间的动摩擦因数μ=
在倾角为θ=30°的足够长的斜面底端,木块A以某一初速度v0沿斜面向上运动,若木块与斜面间的动摩擦因数μ=