题目内容
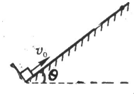 在倾角为θ=30°的足够长的斜面底端,木块A以某一初速度v0沿斜面向上运动,若木块与斜面间的动摩擦因数μ=
在倾角为θ=30°的足够长的斜面底端,木块A以某一初速度v0沿斜面向上运动,若木块与斜面间的动摩擦因数μ=| 1 | ||
2
|
(1)木块A在斜面上离开出发点时和回到出发点时的动能之比
(2)如图所示,在斜面底端安装一固定且垂直于斜面的挡板,不计物块与挡板每次碰撞的机械能损失,求物块以v0=10m/s的初速度沿斜面运动所通过的总路程.
分析:(1)木块向上运动时做匀减速直线运动,向下做匀加速直线运动,分别对这两个过程运用动能定能即可求得答案,要注意两个运动过程中摩擦力做功相等;
(2)根据题意可知,木块最终停在最下端,对全过程运用动能定理即可求出总路程,注意整个过程中只有摩擦力做功,重力做功为零.
(2)根据题意可知,木块最终停在最下端,对全过程运用动能定理即可求出总路程,注意整个过程中只有摩擦力做功,重力做功为零.
解答:解:(1)对向上运动的过程中运用动能定理得:-mgLsinθ-μmgLcosθ=0-EK0
对向下运动的过程中运用动能定理得:mgLsinθ-μmgLcosθ=EK-0
联列可得:
=3
(2)根据题意可知,mgsinθ>μmgcosθ所以木块最终停在最下端,对全过程运用动能定理得:
-μmgcosθs=0-
m v02
解得:s=20m
答:(1)木块A在斜面上离开出发点时和回到出发点时的动能之比为3;(2)物块以v0=10m/s的初速度沿斜面运动所通过的总路程为20m.
对向下运动的过程中运用动能定理得:mgLsinθ-μmgLcosθ=EK-0
联列可得:
| EK0 |
| EK |
(2)根据题意可知,mgsinθ>μmgcosθ所以木块最终停在最下端,对全过程运用动能定理得:
-μmgcosθs=0-
| 1 |
| 2 |
解得:s=20m
答:(1)木块A在斜面上离开出发点时和回到出发点时的动能之比为3;(2)物块以v0=10m/s的初速度沿斜面运动所通过的总路程为20m.
点评:该题要求同学们能够根据解题的需要,选取不同的运动过程运用动能定理解题,要注意重力做功只跟高度差有关,难度不大.

练习册系列答案
相关题目
 如图所示,在倾角为30°的斜面上有一重10N的物块,被平行于斜面大小为8N的恒力F推着沿斜面匀速上行.在推力F突然撤消的瞬间,物块受到的合力大小为( )
如图所示,在倾角为30°的斜面上有一重10N的物块,被平行于斜面大小为8N的恒力F推着沿斜面匀速上行.在推力F突然撤消的瞬间,物块受到的合力大小为( ) 如图所示,在倾角为30°的斜面OA左侧有一竖直档板,档板与斜面OA间有垂直纸面向外的匀强磁场,磁感应强度为B=0.2T,档板上有一小孔P,OP=0.6m,现有一质量m=4×10-20kg,带电量q=+2×10-14C的粒子,从小孔以速度v0=3×104m/s水平射进磁场区域.粒子重力不计.
如图所示,在倾角为30°的斜面OA左侧有一竖直档板,档板与斜面OA间有垂直纸面向外的匀强磁场,磁感应强度为B=0.2T,档板上有一小孔P,OP=0.6m,现有一质量m=4×10-20kg,带电量q=+2×10-14C的粒子,从小孔以速度v0=3×104m/s水平射进磁场区域.粒子重力不计. (2009?深圳一模)如图所示,在倾角为30°的光滑斜面上固定一光滑金属导轨CDEFG,图中OH∥CD∥FG,∠DEF=60°,CD=DE=EF=FG=OE=L;一根质量为m、长度为2L的导体棒AB在电机牵引下,以恒定速度v0沿OH方向从斜面底端滑上导轨并到达斜面顶端,O是AB棒的中点,AB⊥OH.金属导轨的CD、FG段电阻不计,DEF段与AB棒材料与横截面积均相同,单位长度的电阻均为r,整个斜面处在垂直斜面向上、磁感应强度为B的匀强磁场中.求:
(2009?深圳一模)如图所示,在倾角为30°的光滑斜面上固定一光滑金属导轨CDEFG,图中OH∥CD∥FG,∠DEF=60°,CD=DE=EF=FG=OE=L;一根质量为m、长度为2L的导体棒AB在电机牵引下,以恒定速度v0沿OH方向从斜面底端滑上导轨并到达斜面顶端,O是AB棒的中点,AB⊥OH.金属导轨的CD、FG段电阻不计,DEF段与AB棒材料与横截面积均相同,单位长度的电阻均为r,整个斜面处在垂直斜面向上、磁感应强度为B的匀强磁场中.求: 如图,以10m/s的水平初速度抛出的物体,飞行一段时间后,垂直撞在倾角为30?的斜面上,若g取10m/s2,可知物体飞行的时间为( )
如图,以10m/s的水平初速度抛出的物体,飞行一段时间后,垂直撞在倾角为30?的斜面上,若g取10m/s2,可知物体飞行的时间为( ) 如图所示,在倾角为30°的光滑斜面上的O点钉有一根与斜面垂直的钉子,细绳的一端拴在钉子上,绳的另一端拴一个质量为m=0.2kg的小球,绳与斜面平行,小球球心到钉子的距离为R=0.8m.现使小球在斜面上做R为半径的圆周运动,则小球通过最高点时的最小速度大小为
如图所示,在倾角为30°的光滑斜面上的O点钉有一根与斜面垂直的钉子,细绳的一端拴在钉子上,绳的另一端拴一个质量为m=0.2kg的小球,绳与斜面平行,小球球心到钉子的距离为R=0.8m.现使小球在斜面上做R为半径的圆周运动,则小球通过最高点时的最小速度大小为