题目内容
如图甲所示,在倾角为30°的足够长光滑斜面AB前,有一粗糙水平面OA,OA长为4m.有一质量为m的滑块,从O处由静止开始受一水平向右的力F作用.F只在水平面上按图乙所示的规律变化.滑块与OA间的动摩擦因数μ=0.25,g取10m/s2,试求:
(1)滑块到A处的速度大小.
(2)不计滑块在A处的速率变化,滑块冲上斜面的长度是多少?

(1)滑块到A处的速度大小.
(2)不计滑块在A处的速率变化,滑块冲上斜面的长度是多少?

分析:运用动能定理研究O至A的过程,求解A的速度.要注意O至A过程中力是变化的.
运用动能定理研究A点到上滑的最大距离处,求出最大距离.
运用动能定理研究A点到上滑的最大距离处,求出最大距离.
解答:解:(1)由题图乙知,在前2 m内,F1=2mg,做正功;在第3 m内,F2=-0.5mg,做负功;
在第4 m内,F3=0.
滑动摩擦力
f=-μmg=-0.25mg,始终做负功.
对OA过程由动能定理列式得
F1x1+F2x2+fx=
mvA2-0
即2mg×2-0.5mg×1-0.25mg×4=
mvA2,
解得vA=5
m/s.
(2)冲上斜面的过程,由动能定理得
-mg?L?sin30°=0-
mvA2,
所以冲上斜面AB的长度L=5 m.
答:(1)滑块到A处的速度大小为5
m/s.
(2)不计滑块在A处的速率变化,滑块冲上斜面的长度是5m.
在第4 m内,F3=0.
滑动摩擦力
f=-μmg=-0.25mg,始终做负功.
对OA过程由动能定理列式得
F1x1+F2x2+fx=
| 1 |
| 2 |
即2mg×2-0.5mg×1-0.25mg×4=
| 1 |
| 2 |
解得vA=5
| 2 |
(2)冲上斜面的过程,由动能定理得
-mg?L?sin30°=0-
| 1 |
| 2 |
所以冲上斜面AB的长度L=5 m.
答:(1)滑块到A处的速度大小为5
| 2 |
(2)不计滑块在A处的速率变化,滑块冲上斜面的长度是5m.
点评:了解研究对象的运动过程是解决问题的前提,根据题目已知条件和求解的物理量选择物理规律解决问题.
一个题目可能需要选择不同的过程多次运用动能定理研究.
一个题目可能需要选择不同的过程多次运用动能定理研究.

练习册系列答案
相关题目
 如图甲所示,在倾角为θ的光滑斜面上,有一个质量为m的物体在沿斜面方向的力F的作用下由静止开始运动,物体的机械能E随距离x的变化关系如图乙所示.其中0~x1过程的图线是直线,x1~x3过程的图线是曲线,则下列说法中正确的是( )
如图甲所示,在倾角为θ的光滑斜面上,有一个质量为m的物体在沿斜面方向的力F的作用下由静止开始运动,物体的机械能E随距离x的变化关系如图乙所示.其中0~x1过程的图线是直线,x1~x3过程的图线是曲线,则下列说法中正确的是( )| A、在0~x1过程中,物体的速度一直减小 | B、在x1~x2过程中,物体的加速度逐渐变大 | C、在x2~x3过程中,物体的加速度逐渐变小 | D、在x2~x3过程中,合力对物体做正功 |
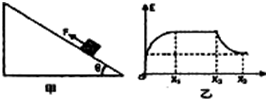 如图甲所示,在倾角为θ的光滑斜面上,有一个质量为m的物体受到一个沿斜面向上的变力F作用下,由静止开始运动.物体的机械能E随路程x的变化关系如图乙所示,其中0-xl、x2-x3过程的图线是曲线,x1-x2过程的图线为平行于x轴的直线,且x=0处曲线的切线斜率与x1=x2处曲线的切线斜率相等.则下列说法中正确的是( )
如图甲所示,在倾角为θ的光滑斜面上,有一个质量为m的物体受到一个沿斜面向上的变力F作用下,由静止开始运动.物体的机械能E随路程x的变化关系如图乙所示,其中0-xl、x2-x3过程的图线是曲线,x1-x2过程的图线为平行于x轴的直线,且x=0处曲线的切线斜率与x1=x2处曲线的切线斜率相等.则下列说法中正确的是( )| A、物体一直沿斜面向上运动 | B、在0-x1过程中,物体的加速度大小先减小后增大 | C、在x1-x2过程中物体的重力势能一直在增加 | D、在x2-x3过程中物体的动能先减少后增加 |
 (2009?盐城一模)如图甲所示,在倾角为30°的足够长的光滑斜面上,有一质量为m的物体,受到沿斜面方向的力F作用,力F按图乙所示规律变化(图中纵坐标是F与mg的比值,力沿斜面向上为正).则物体运动的速度v随时间t变化的规律是下图中的(物体的初速度为零,重力加速度取10m/s2)( )
(2009?盐城一模)如图甲所示,在倾角为30°的足够长的光滑斜面上,有一质量为m的物体,受到沿斜面方向的力F作用,力F按图乙所示规律变化(图中纵坐标是F与mg的比值,力沿斜面向上为正).则物体运动的速度v随时间t变化的规律是下图中的(物体的初速度为零,重力加速度取10m/s2)( )
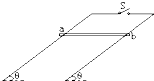 如图甲所示,在倾角为θ的斜面上固定有两根足够长的平行光滑导轨,轨距为L,金属导体棒ab垂直于两根轨道放在导轨上,导体ab的质量为m,电阻为R,导轨电阻不计,空间有垂直于导轨平面的匀强磁场,磁感应强度为B.当金属导体ab由静止开始向下滑动一段时间t0,再接通开关S,则关于导体ab运动的v-t图象可能正确的是( )
如图甲所示,在倾角为θ的斜面上固定有两根足够长的平行光滑导轨,轨距为L,金属导体棒ab垂直于两根轨道放在导轨上,导体ab的质量为m,电阻为R,导轨电阻不计,空间有垂直于导轨平面的匀强磁场,磁感应强度为B.当金属导体ab由静止开始向下滑动一段时间t0,再接通开关S,则关于导体ab运动的v-t图象可能正确的是( )