题目内容
质量为m的物体以速度v0从地面竖直上抛,当它运动到离地面h高处时,它的动能和势能正好相等,这个高度是h= (不计空气阻力,重力加速度为g)
分析:竖直上抛运动在运动过程中只有重力做功,机械能守恒,可用机械能守恒和动能和势能相等的条件,列式求解h.
解答:解:竖直上抛运动在运动过程中只有重力做功,机械能守恒,选地面为零势能面.
抛出时的机械能为:E1=
m
高为h处的机械能为:E2=mgh+
mv2
由机械能守恒得:E1=E2,即得
m
=mgh+
mv2
又根据已知条件知,mgh=
mv2
联立以上两式解得:h=
故答案为:
抛出时的机械能为:E1=
| 1 |
| 2 |
| v | 2 0 |
高为h处的机械能为:E2=mgh+
| 1 |
| 2 |
由机械能守恒得:E1=E2,即得
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
又根据已知条件知,mgh=
| 1 |
| 2 |
联立以上两式解得:h=
| ||
| 4g |
故答案为:
| ||
| 4g |
点评:对于竖直上抛运动的能量问题,关键要掌握机械能守恒,但不能将mgh=
mv2式子当成机械能守恒.
| 1 |
| 2 |

练习册系列答案
相关题目
 质量为m的物体以速度v0从地面竖直上抛,若以地面为参考平面,则上升的最大高度H为多少?当物体的动能和重力势能相等时物体距离地面的高度h又是多少?(不计空气阻力).
质量为m的物体以速度v0从地面竖直上抛,若以地面为参考平面,则上升的最大高度H为多少?当物体的动能和重力势能相等时物体距离地面的高度h又是多少?(不计空气阻力).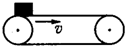 如图所示,质量为m的物体以速度v水平向右冲上一水平传送带.传送带由电动机带动,始终保持3v的速率顺时针运动,物体与传送带间的动摩擦因数为μ,物体过一会儿能保持与传送带相对静止,对于物体从冲上传送带到相对传送带静止这一过程,摩擦力对物体做的功为
如图所示,质量为m的物体以速度v水平向右冲上一水平传送带.传送带由电动机带动,始终保持3v的速率顺时针运动,物体与传送带间的动摩擦因数为μ,物体过一会儿能保持与传送带相对静止,对于物体从冲上传送带到相对传送带静止这一过程,摩擦力对物体做的功为