��Ŀ����
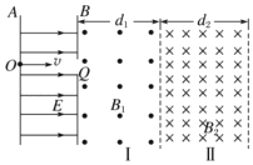
����Ŀ����ͼ����ƽ�н�����A��B����Ʋ�U��5��104V����B���Ҳ�����������ͬ��������ͬ���н�ų������������ǿ���Ϊd1��d2��6.25m���Ÿ�Ӧǿ�ȷֱ�ΪB1��2.0T��B2��4.0T��������ͼ����ʾ������һ����m��1.0��10��8kg�������q��1.6��10��6C���������Բ��Ƶ����Ӵ�A���O���ɾ�ֹ�ͷţ��������ٺ�ǡ�ô�B���С��Q���ɳ�������
��1���������ӴӼ��ٵ糡Q���ɳ�ʱ���ٶ�v�Ĵ�С��
��2���������Ӵ����ų����������õ�ʱ��t��
��3����d1�Ŀ��Ȳ��䣬�ı�d2�Ŀ��ȣ�Ҫʹ���Ӳ��ܴ������ɳ��ų�����d2�Ŀ�������Ϊ���
���𰸡���1��4.0��103 m/s ��2��![]() s ��3��9.375 m
s ��3��9.375 m
��������
��1�������ڵ糡�����ȼ���ֱ���˶����ɶ��ܶ����У�
![]()
��ã�v��4.0��103 m/s
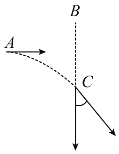
��2�������˶��켣��ͼ���������ڴų��������������Բ���˶��İ뾶Ϊr�������������ṩ�������ã�
![]()
�������ݽ�ã�r��12.5 m
�������ڢ�������Բ���˶���Բ�Ľ�Ϊ������
![]()
��������30��
�����ڢ����˶�����
![]()
�������ڢ����˶�ʱ��
![]()
��ã�![]() ��
��
��3���������ڢ�����Բ���˶��Ĺ���뾶ΪR�����У�
![]()
��ã�R��6.25 m
Ҫʹ���Ӳ��ܴӢ����ɳ��ų��������˶��Ĺ켣��ų��߽�����ʱ��

��ͼ��֪�����ų��Ŀ�������Ϊ��
d2��R+Rcos 60�㣽1.5R��9.375 m

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�