题目内容
为了测量蹦床运动员从蹦床上跃起的高度,探究小组设计了如下的方法:他们在蹦床的弹性网上安装压力传感器,利用传感器记录运动员在运动过程中对弹性网的压力,来推测运动员跃起的高度。右图为某段时间内蹦床运动员的压力—时间图象。运动员在空中仅在竖直方向上运动,且可视为质点,则可估算出运动员在这段时间内跃起的最大高度为(g取10m/s2)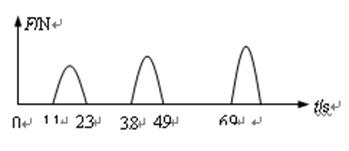
| A.1.5m | B.1. 8m |
| C.5.0m | D.7.2m |
C
解析试题分析:当蹦床的压力为0时,即运动员在空中,当再次出现压力时,说明运动员再次落回蹦床,观察图像,从离开蹦床到落回蹦床,运动员在空中运动时间最长为为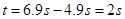 ,此时上升的高度最高。根据上升下降的对称性,下降的最长时间为
,此时上升的高度最高。根据上升下降的对称性,下降的最长时间为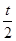 ,最大高度
,最大高度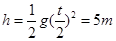 ,对照选项C对。
,对照选项C对。
考点:竖直上抛运动

练习册系列答案
相关题目
(多选)将甲乙两小球先后以同样的速度在距地面不同高度处竖直向上抛出,抛出时间相隔2 s,它们运动的图像分别如直线甲乙所示。则( )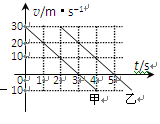
| A.t=2 s时,两球的高度相差一定为40 m |
| B.t=4 s时,两球相对于各自的抛出点的位移相等 |
| C.两球从抛出至落到地面所用的时间间隔相等 |
| D.甲球从抛出至到达最高点的时间间隔与乙球相等 |
2008年北京奥运会上何雯娜夺得中国首枚奥运会女子蹦床金牌。为了测量运动员跃起的高度,可在弹性网上安装压力传感器,利用传感器记录运动员运动过程中对弹性网的压力,并由计算机作出压力-时间图象,如图所示。运动员在空中运动时可视为质点,则可求运动员跃起的最大高度为(g取10m/s2)( )
| A.7.2m | B.5.0m | C.1.8m | D.1.5m |
某物体以30 m/s的初速度竖直上抛,不计空气阻力,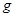 取
取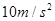 .5s内物体的( )
.5s内物体的( )
| A.路程为65m |
| B.位移大小为25m,方向向下 |
| C.速度改变量的大小为10m/s |
| D.平均速度大小为13m/s,方向向上 |
在某高处A点,以大小为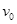 的速度同时竖直向上和向下抛出a、b两球,不计空气阻力,则下列说法中正确的是
的速度同时竖直向上和向下抛出a、b两球,不计空气阻力,则下列说法中正确的是
A.两球落地的时间差为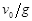 |
B.两球落地的时间差为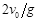 |
C.两球落地的时间差为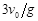 |
| D.两球落地的时间差与高度有关 |
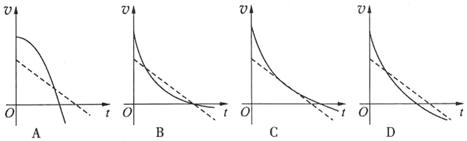
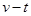 图像可能正确的是
图像可能正确的是