��Ŀ����
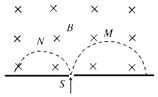
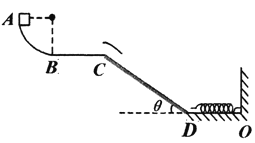
����Ŀ����ͼ��������Ա���о�ij�˶�����·������ʱ����һ����m��lkgС���飨��Ϊ�ʵ㣩�ڰ뾶R��0.4m��![]() Բ��A���ɾ�ֹ�ͷţ��˶���B��ʱ�ٶ�Ϊv��2m�Ms������B��������Բ�������ȥ�������ڿ���Ϊ�⻬���ϵ�ˮƽ�����˶�һ�ξ����ͨ����������C����ɵ����Ϊ����37�㡢��s��lmб����CD�ϣ�CD֮������һ������������ϣ����뻬���Ķ�Ħ��ϵ������0������1.5֮����ڡ�б��ײ�D����⻬����ƽ��������������һ���ᵯ��һ�˹̶���O�㣬��Ȼ״̬����һ��ǡ����D�㡣��Ϊ����ͨ��C��Dǰ���ٶȴ�С���䣬���Ħ�������ڻ���Ħ������ȡg��10m/s2��sin37�㣽0.6��cos37�㣽0.8�����ƿ���������
Բ��A���ɾ�ֹ�ͷţ��˶���B��ʱ�ٶ�Ϊv��2m�Ms������B��������Բ�������ȥ�������ڿ���Ϊ�⻬���ϵ�ˮƽ�����˶�һ�ξ����ͨ����������C����ɵ����Ϊ����37�㡢��s��lmб����CD�ϣ�CD֮������һ������������ϣ����뻬���Ķ�Ħ��ϵ������0������1.5֮����ڡ�б��ײ�D����⻬����ƽ��������������һ���ᵯ��һ�˹̶���O�㣬��Ȼ״̬����һ��ǡ����D�㡣��Ϊ����ͨ��C��Dǰ���ٶȴ�С���䣬���Ħ�������ڻ���Ħ������ȡg��10m/s2��sin37�㣽0.6��cos37�㣽0.8�����ƿ���������
��1������B��ʱ�Թ����ѹ����С�Լ���AB�Ͽ˷����������Ĺ���
��2������������0.5�����ʵ��C�˶���һ���˶���D���ʱ�䣻
��3�������ջ���ͣ��D�㣬�����Ŀ���ȡֵ��Χ��
���𰸡���1��20N,2J��2����![]() ��1��s��3��
��1��s��3��![]() ������
������![]() ��������1
��������1
��������
��1��������B�㣬�ܵ�������֧��������B�㣬����ţ�ٵڶ������У�![]() ��
��
�������ݽ�ã�F��20N��
��ţ�ٵ������ɵã�![]() ��20N��
��20N��
��A��B���ɶ��ܶ����ã�mgR��W��![]() mv2��
mv2��
�������ݵã�W��2J��
��2����CD���˶�����ţ�ٵڶ����ɵã�mgsin������mgcos����ma��
��ã�a��6m/s2��
�����ȱ����˶������У�![]()
�������ݽ�ã�t����![]() ��1��s
��1��s
��3�����ջ���ͣ��D�������ֿ��ܣ�
A������ǡ�ô�C�»���D���ɶ��ܶ����ã�mgssin������mgcos����0-![]()
������1
B��������б��CD��ˮƽ������������˶������վ�ֹ��D�㡣
������ǡ���ܷ���C���ɳ����ɶ��ܶ����ã�����1mgcos��2s��0��![]() ��
��
����1��![]()
������ǡ���ܾ�ֹ��б���ϣ�����mgsin������2mgcos��
����2��![]()
����![]() ������
������![]() ��������1
��������1