题目内容
 (2011?河南模拟)如图所示、传送带的水平部分AB长为=5米,以V0=4m/s的速度向右匀速运动,水平台面与传送带平滑连接与B点,BC长S=1米,台面右边有高为h=0.5m的光滑曲面CD.一质量m=1kg的工件(可以视为质点),从A点无初速度释放,工件与传送带及台面间的动摩擦因数均为0.2,g=10m/s2,求:
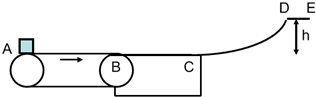
(2011?河南模拟)如图所示、传送带的水平部分AB长为=5米,以V0=4m/s的速度向右匀速运动,水平台面与传送带平滑连接与B点,BC长S=1米,台面右边有高为h=0.5m的光滑曲面CD.一质量m=1kg的工件(可以视为质点),从A点无初速度释放,工件与传送带及台面间的动摩擦因数均为0.2,g=10m/s2,求:(1)工件运动到B点时的速度大小
(2)通过计算说明,工件能否通过D点到达上平台DE上.
分析:对工件正确受力分析,找出工件的合力,明确其运动性质,运用牛顿第二定律和运动学公式去求解B点时的速度.
关于工件能否通过D点到达上平台DE上?我们运用动能地理可以先求出工件沿曲面CD上升的最大高度(到达最大高度速度为0),然后与题目的D点高度对比.
关于工件能否通过D点到达上平台DE上?我们运用动能地理可以先求出工件沿曲面CD上升的最大高度(到达最大高度速度为0),然后与题目的D点高度对比.
解答:解:(1)工件刚放上时,做初速度为零的匀加速直线运动,
由牛顿第二定律得:μmg=ma
解得:a=2m/s2
当两者速度相等时,t=
=2s.
工件对地的位移为:s1=
at2=4m<L
工件速度达到4m/s时,即与传送带相对静止,之后不受传送带的摩擦力做匀速直线运动.
因此,工件到达B点的速度为:vB=4m/s.
(2)设工件沿曲面CD上升的最大高度为h′,
由动能定理得:μmgs1-μmgs-mgh′=0
解得:h′=0.6m>h
所以,工件能够通过D点到达平台DE上.
答:(1)工件运动到B点时的速度大小为4m/s.
(2)工件能够通过D点到达平台DE上.
由牛顿第二定律得:μmg=ma
解得:a=2m/s2
当两者速度相等时,t=
| v0 |
| a |
工件对地的位移为:s1=
| 1 |
| 2 |
工件速度达到4m/s时,即与传送带相对静止,之后不受传送带的摩擦力做匀速直线运动.
因此,工件到达B点的速度为:vB=4m/s.
(2)设工件沿曲面CD上升的最大高度为h′,
由动能定理得:μmgs1-μmgs-mgh′=0
解得:h′=0.6m>h
所以,工件能够通过D点到达平台DE上.
答:(1)工件运动到B点时的速度大小为4m/s.
(2)工件能够通过D点到达平台DE上.
点评:对应传送带的问题要正确受力分析特别是摩擦力的分析,要注意工件和传送带的相对运动,根据要求的物理量选择物理规律去解决.关于能否通过D点到达平台DE上,我们可以按解答中做,也可以求出假设到达D点,在B点至少有多大的速度,再与题目中B的实际速度对比.

练习册系列答案
相关题目
 (2011?河南模拟)已知一个标有“2.4V、0.06A”电学元件的R-U特性如图所示.某同学想利用下列可供选择的实验器材,设计一个电路验证该元件的电阻R随电压U变化的图象.
(2011?河南模拟)已知一个标有“2.4V、0.06A”电学元件的R-U特性如图所示.某同学想利用下列可供选择的实验器材,设计一个电路验证该元件的电阻R随电压U变化的图象. (2011?河南模拟)如图所示,两物体A、B叠放在光滑水平面上,mA=mB=1kg,A、B间动摩擦因数μ=0.4,现对物体A施加一水平力F,F-t关系图象如图所示.两物体在力F作用下由静止开始运动,且B物体足够长.若向右为正方向,则对物体的运动,下列说法正确的是( )
(2011?河南模拟)如图所示,两物体A、B叠放在光滑水平面上,mA=mB=1kg,A、B间动摩擦因数μ=0.4,现对物体A施加一水平力F,F-t关系图象如图所示.两物体在力F作用下由静止开始运动,且B物体足够长.若向右为正方向,则对物体的运动,下列说法正确的是( )