题目内容
如图所示，在一足够大的空间内存在着水平向右的匀强电场，电场强度大小E＝3.0×104N/C。有一个质量m＝4.0×10－3kg的带电小球，用绝缘轻细线悬挂起来，静止时细线偏离竖直方向的夹角θ＝37°。取g＝10m/s2，sin37°＝0.60，cos37°＝0.80，不计空气阻力的作用。求：
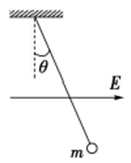
(1)求小球所带的电荷量及电性；
(2)如果将细线轻轻剪断，求细线剪断后，小球运动的加速度大小；
(3)从剪断细线开始经过时间t＝0.20s，求这段时间内小球电势能的变化量。
(1)求小球所带的电荷量及电性；
(2)如果将细线轻轻剪断，求细线剪断后，小球运动的加速度大小；
(3)从剪断细线开始经过时间t＝0.20s，求这段时间内小球电势能的变化量。
(1)1.0×10－6C正电 (2)12.5m/s2 (3)4.5×10－3J
试题分析：(1)小球受到重力mg、电场力F和细线的拉力T的作用，由共点力平衡条件，得
F＝qE＝mgtanθ
解得q＝mgtanθ/E＝1.0×10－6C
电场力的方向与电场强度的方向相同，故小球所带电荷为正电荷
(2)剪断细线后，小球做匀加速直线运动，设其加速度为a，由牛顿第二定律，得
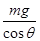＝ma解得 a＝
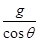＝12.5m/s2(3)在t＝0.20s的时间内，小球的位移为
l＝
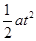＝0.25m小球运动过程中，电场力做的功
W＝qElsinθ＝mglsinθtanθ＝4.5×10－3J
所以小球电势能的变化量(减少量)ΔEp＝4.5×10－3J。
点评：本题的综合性较强，关键是根据受力分析，结合牛顿第二定律解题
练习册系列答案
相关题目
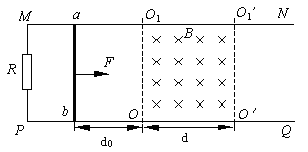
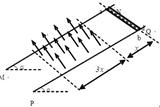
，方向垂直纸面向里．现有带正电的粒子连续不断地以速度
，沿两板间的中线
平行金属板射入电场中，磁场边界MN与中线
，粒子所受的重力和粒子间的相互作用力均忽略不计．
时刻射入电场的带电粒子恰能从平行金属板边缘射出，求该带电粒子射出电场时的速度大小．
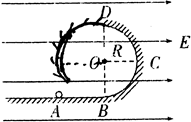
圆周离开电磁场区域，沿y轴负方向运动，然后从x轴上的K点进入第四象限。小球P、Q相遇在第四象限的某一点，且竖直方向速度相同。设运动过程中小球P电量不变，小球P和Q始终在纸面内运动且均看作质点，重力加速度为g。求：
）从直角坐标系xOy平面内的坐标原点O以很小的速度进入匀强电场E1，计算时不计此速度且只考试xOy平面内的运动。求：
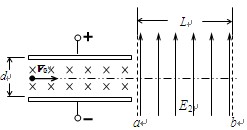
带电量为+q的带电粒子，以水平速度v0从平行金属板的正中间射入并做匀速直线运动，然后又垂直射入场强大小为E2，方向竖直向上的匀强电场，其边界a、b间的宽为L(该电场竖直方向足够长)．电场和磁场都有理想边界，且粒子所受重力不计，求：
