题目内容
15. 如图所示,间距为L,电阻不计的足够长平行光滑金属导轨水平放置,导轨左端用一阻值为R的电阻连接,导轨上横跨一根质量为m,电阻也为R的金属棒,金属棒与导轨接触良好.整个装置处于竖直向上、磁感应强度为B的匀强磁场中,现使金属棒以初速度v0沿导轨向右运动,若金属棒在整个运动过程中通过的电荷量为q.下列说法正确的是( )
如图所示,间距为L,电阻不计的足够长平行光滑金属导轨水平放置,导轨左端用一阻值为R的电阻连接,导轨上横跨一根质量为m,电阻也为R的金属棒,金属棒与导轨接触良好.整个装置处于竖直向上、磁感应强度为B的匀强磁场中,现使金属棒以初速度v0沿导轨向右运动,若金属棒在整个运动过程中通过的电荷量为q.下列说法正确的是( )| A. | 金属棒在导轨上做匀减速运动 | |
| B. | 整个过程中电阻R上产生的焦耳热为$\frac{m{{v}_{0}}^{2}}{2}$ | |
| C. | 整个过程中金属棒在导轨上发生的位移为$\frac{2qR}{BL}$ | |
| D. | 整个过程中金属棒克服安培力做功为$\frac{m{{v}_{0}}^{2}}{2}$ |
分析 对金属棒进行受力分析,求出金属棒受到的合外力,然后判断金属棒的运动性质;
由动能定理求出克服安培力所做的功;
求出感应电荷量的表达式,然后求出金属棒的位移;
由能量守恒定律和串联电路的特点求出电阻R上产生的焦耳热.
解答 解:金属棒在整个运动过程中,受到竖直向下的重力,竖直向上的支持力,这两个力合力为零,受到水平向左的安培力,金属棒受到的合力为安培力;
A、金属棒受到的安培力F=BIL=BL$\frac{E}{2R}$=BL$\frac{BL{v}_{0}}{2R}=\frac{{B}^{2}{L}^{2}{v}_{0}}{2R}$,金属棒受到安培力作用而做减速运动,速度v不断减小,安培力不断减小,加速度不断减小,故金属棒做加速度逐渐减小的变减速运动,故A错误;
B、克服安培力做功把金属棒的动能转化为焦耳热,由于金属棒电阻与电阻串联在电路中,且阻值相等,则电阻R上产生的焦耳热Q=$\frac{1}{2}$W安=$\frac{1}{4}$mv02,故B错误;
C、整个过程中感应电荷量q=I△t=$\frac{E}{2R}$△t,又E=$\frac{△Φ}{△t}$=$\frac{BLs}{△t}$,
联立得:q=$\frac{BLs}{2R}$
故金属棒的位移s=$\frac{2qR}{BL}$,故C正确;
D、整个过程中由动能定理可得:-W安=0-$\frac{1}{2}$mv02,金属棒克服安培力做功为W安=$\frac{m{{v}_{0}}^{2}}{2}$,故D正确;
故选:CD.
点评 金属棒在运动过程中克服安培力做功,把金属棒的动能转化为焦耳热,在此过程中金属棒做加速度减小的减速运动;对棒进行受力分析、熟练应用法拉第电磁感应定律、欧姆定律、动能定理等正确解题

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
5.关于质点作匀速圆周运动的下列说法,正确的是( )
| A. | 线速度v与角速度ω不变 | B. | 质点的动能Ek一定不变 | ||
| C. | 合外力F合与加速度a不变 | D. | 质点的机械能E一定不变 |
6.对于红、绿、蓝三种单色光,下列表述正确的是( )
| A. | 红光频率最高 | B. | 蓝光频率最高 | ||
| C. | 绿光光子能量最小 | D. | 蓝光光子能量最小 |
3. 如图所示,圆形区域内有垂直于纸面的匀强磁场,三个质量和电荷量都相同的带电粒子a、b、c,以不同速率对准圆心O沿着AO方向射入磁场,其运动轨迹如图.若带电粒子只受磁场力作用,则下列说法正确的是( )
如图所示,圆形区域内有垂直于纸面的匀强磁场,三个质量和电荷量都相同的带电粒子a、b、c,以不同速率对准圆心O沿着AO方向射入磁场,其运动轨迹如图.若带电粒子只受磁场力作用,则下列说法正确的是( )
 如图所示,圆形区域内有垂直于纸面的匀强磁场,三个质量和电荷量都相同的带电粒子a、b、c,以不同速率对准圆心O沿着AO方向射入磁场,其运动轨迹如图.若带电粒子只受磁场力作用,则下列说法正确的是( )
如图所示,圆形区域内有垂直于纸面的匀强磁场,三个质量和电荷量都相同的带电粒子a、b、c,以不同速率对准圆心O沿着AO方向射入磁场,其运动轨迹如图.若带电粒子只受磁场力作用,则下列说法正确的是( )| A. | a粒子动能最大 | |
| B. | c粒子速率最大 | |
| C. | a粒子在磁场中运动时间最长 | |
| D. | 它们做圆周运动的周期关系有Ta<Tb<Tc |
20. 在某一均匀介质中由波源O发出的简谐波在x轴上传播,某时刻的波形如图,其波速为5m/s,则下列说法正确的是( )
在某一均匀介质中由波源O发出的简谐波在x轴上传播,某时刻的波形如图,其波速为5m/s,则下列说法正确的是( )
 在某一均匀介质中由波源O发出的简谐波在x轴上传播,某时刻的波形如图,其波速为5m/s,则下列说法正确的是( )
在某一均匀介质中由波源O发出的简谐波在x轴上传播,某时刻的波形如图,其波速为5m/s,则下列说法正确的是( )| A. | 此时P、Q两点运动方向相同 | |
| B. | 再经过0.5s质点N刚好在(-5m,20cm)位置 | |
| C. | 能与该波发生干涉的横波的频率一定为3HZ | |
| D. | 波的频率与振源的振动频率相同 | |
| E. | 再经过0.6s质点P传到N点 |
7. 如图所示的曲线是某个质点在恒力作用下的一段运动轨迹.质点从M点出发经P点到达N 点,已知弧长MP大于弧长PN,质点由M点运动到P点与从P点运动到N点的时间相等.下列说法中正确的是( )
如图所示的曲线是某个质点在恒力作用下的一段运动轨迹.质点从M点出发经P点到达N 点,已知弧长MP大于弧长PN,质点由M点运动到P点与从P点运动到N点的时间相等.下列说法中正确的是( )
 如图所示的曲线是某个质点在恒力作用下的一段运动轨迹.质点从M点出发经P点到达N 点,已知弧长MP大于弧长PN,质点由M点运动到P点与从P点运动到N点的时间相等.下列说法中正确的是( )
如图所示的曲线是某个质点在恒力作用下的一段运动轨迹.质点从M点出发经P点到达N 点,已知弧长MP大于弧长PN,质点由M点运动到P点与从P点运动到N点的时间相等.下列说法中正确的是( )| A. | 质点从M到N过程中速度大小保持不变 | |
| B. | 质点在这两段时间内的速度变化量大小相等,方向相同 | |
| C. | 质点在这两段时间内的速度变化量大小不相等,方向相同 | |
| D. | 质点在MN间的运动是加速运动 |
 ”表示).
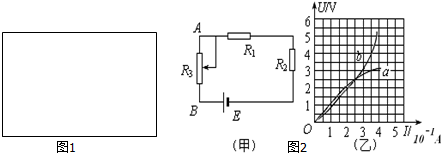
”表示). 甲、乙两质点在同一时刻、从同一地点沿同一方向做直线运动.质点甲做初速度为零,加速度大小为a1的匀加速直线运动,质点乙做初速度为v0,加速度大小为a2的匀减速直线运动至速度减为零保持静止,甲、乙两质点在运动过程中的位置x-速度v图象如图所示,虚线与对应的坐标轴垂直.
甲、乙两质点在同一时刻、从同一地点沿同一方向做直线运动.质点甲做初速度为零,加速度大小为a1的匀加速直线运动,质点乙做初速度为v0,加速度大小为a2的匀减速直线运动至速度减为零保持静止,甲、乙两质点在运动过程中的位置x-速度v图象如图所示,虚线与对应的坐标轴垂直.