题目内容
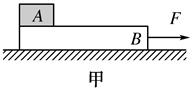
某游乐场开发了一个名为“翻天滚地”的游乐项目。原理图如图所示:一个 圆弧形光滑圆管轨道ABC,放置在竖直平面内,轨道半径为R,在A 点与水平地面AD相接,B点为圆轨道最低点,地面与圆心O等高,MN 是放在水平地面上长为3R、厚度不计的减振垫,左端M正好位于A点。让游客进入一个中空的透明弹性球,人和球的总质量为m,球的直径略小于圆管直径。将球(内装有参与者)从A处管口正上方某处由静止释放后,游客将经历一个“翻天滚地”的刺激过程,不考虑空气阻力,球视为质点。那么以下说法中正确的是
圆弧形光滑圆管轨道ABC,放置在竖直平面内,轨道半径为R,在A 点与水平地面AD相接,B点为圆轨道最低点,地面与圆心O等高,MN 是放在水平地面上长为3R、厚度不计的减振垫,左端M正好位于A点。让游客进入一个中空的透明弹性球,人和球的总质量为m,球的直径略小于圆管直径。将球(内装有参与者)从A处管口正上方某处由静止释放后,游客将经历一个“翻天滚地”的刺激过程,不考虑空气阻力,球视为质点。那么以下说法中正确的是
A.要使球能从C点射出后能打到垫子上,则球经过C点时的速度至少为 |
| B.球从A到B的过程中重力的功率先减小后增大 |
C.若球从C点射出后恰好能打到垫子的M端,则球经过C点时对管外壁压力大小为 |
| D.要使球能通过C点落到垫子上,球离A点的最大高度是5R |
D
解析试题分析:在A中,要使球能从C点射出后能打到垫子上,根据平抛运动的规律,其水平射程要达到R,由于小球从C点射出后其下落的时间为t=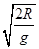 ,水平运行的位移为R,则其水平的速度为v=
,水平运行的位移为R,则其水平的速度为v=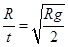 ,故A是不对的;
,故A是不对的;
在B中球从A到B的过程中重力的大小是不变的,而其速度又逐渐增大,即其重力的功率应该逐渐增大,B是不对的;
在C中,若球从C点射出后恰好能打到垫子的M端,则其射出C点速度大小为v=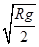 ,而由牛顿么二定律可得,mg=
,而由牛顿么二定律可得,mg=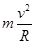 ,小球从C点射出时对管壁无压力的速度为
,小球从C点射出时对管壁无压力的速度为 ,而现在的速度小于它,则球经过C点时它应该对对管的内壁产生压力,所以C是不对的;
,而现在的速度小于它,则球经过C点时它应该对对管的内壁产生压力,所以C是不对的;
在D中,求最大高度时,就是小球从C点射出后落到垫子的最右端时,水平射程为4R,则射出C点的速度为v′=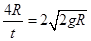 ,则根据机械能守恒定律得:mgH=mgR+
,则根据机械能守恒定律得:mgH=mgR+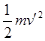 ,代入计算可得H=5R,故D是正确的。
,代入计算可得H=5R,故D是正确的。
考点:牛顿第二定律,机械能守恒定律。

如图所示,倾角为30°的光滑杆上套有一个小球和两根轻质弹簧,两弹簧的一端各与小球相连,另一端分别用销钉M、N固定于杆上,小球处于静止状态.设拔去销钉M(撤去弹簧a)瞬间,小球的加速度大小为6m/s2.若不拔去销钉M,而拔去销钉N(撤去弹簧b)瞬间,小球的加速度可能是(g取10m/s2):( )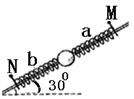
| A.11m/s2,沿杆向上 | B.11m/s2,沿杆向下 |
| C.1m/s2,沿杆向上 | D.1m/s2,沿杆向下 |
如图,质量为MA、MB的A、B两小球分别连在弹簧两端,B端用细线固定在倾角为30°的光滑斜面上,若不计弹簧质量,在线被剪断瞬间,A、B两球的加速度分别为( )
A.0和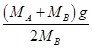 B.
B. 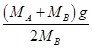 和0
和0
C. 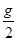 和0 D.都等于
和0 D.都等于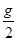
如图所示,在光滑平面上有一静止小车,小车质量为M=5kg,小车上静止地放置着质量为m=1kg的木块,木块和小车间的动摩擦因数为μ=0.2,用水平恒力F拉动小车,下列关于木块的加速度am和小车的加速度aM,可能正确的有:
| A.am=2m/s2, aM=1 m/s2 |
| B.am=1m/s2, aM=2 m/s2 |
| C.am=2m/s2, aM=4 m/s2 |
| D.am=3m/s2, aM=5 m/s2 |
如图1所示,在粗糙程度处处相同的水平地面上,物块在水平向右的力F作用下由静止开始运动。运动的速度v与时间t的关系如图2所示。由图象可知,
| A.在2s—4s内,力F=0 |
| B.在4s—6s内,力F=0 |
| C.在0—2s内,力F逐渐变小 |
| D.在0—2s内,力F逐渐增大 |
有一辆质量为170kg、额定功率为1440W的太阳能试验汽车,安装有约6m2的太阳能电池板和蓄能电池,该电池板在有效光(垂直照射在电池板上的太阳光)照射条件下单位面积输出的电功率为30W/ m2。若驾驶员的质量为70kg,汽车最大行驶速度为90km/h。假设汽车行驶时受到的空气阻力与其速度成正比,则汽车( )
| A.以最大速度行驶时牵引力大小为57.6N |
| B.以额定功率启动时的加速度大小为0.24 m/s2 |
| C.保持最大速度行驶1 h至少需要有效光照8 h |
| D.直接用太阳能电池板提供的功率可获得3.13 m/s的最大行驶速度 |
如右图所示,自由下落的小球下落一段时间后,与弹簧接触,从它接触弹簧开始,到弹簧压缩到最短的过程中,则( )
| A.小球立即做减速运动 |
| B.小球一直做加速运动且加速度不变 |
| C.小球所受的弹簧弹力等于重力时,小球速度最大 |
| D.当弹簧处于最大压缩量时,小球的加速度方向向上 |