题目内容
【题目】如图所示,质量均为m的木块A和B用一轻弹簧相连,竖直放在光滑的水平面上,木块A上放有质量为2m的木块C,三者均处于静止状态.现将木块C迅速移开,若重力加速度为g,则在木块C移开的瞬间( )
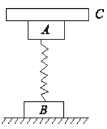
A. 弹簧的形变量不改变
B. 弹簧的弹力大小为mg
C. 木块A的加速度大小为2g
D. 木块B对水平面的压力迅速变为2mg
【答案】AC
【解析】
原来系统静止,根据共点力平衡求出弹簧的弹力。在将C迅速移开的瞬间,弹簧的弹力不变,根据牛顿第二定律求出木块A的加速度。对B,由平衡条件分析地面对B的支持力,从而分析出B对地面的压力。
A项:由于弹簧弹力属于渐变,所以撤去C的瞬间,弹簧的形变量不变,故A正确;
B项:开始整体处于平衡状态,弹簧的弹力等于A和C的重力,即F=3mg,撤去C的瞬间,弹簧的形变量不变,弹簧的弹力不变,仍为3mg,故B错误;
C项:撤去C瞬间,弹力不变,A的合力等于C的重力,对木块A,由牛顿第二定律得:2mg=ma,解得:a=2g,方向竖直向上,故C正确;
D项:撤去C的瞬间,弹簧的弹力不变,仍为3mg,对B,由平衡条件得:F+mg=N,解得:N=4mg,木块B对水平面的压力为4mg,故D错误。
故选:AC。

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目