题目内容
(2009?巢湖一模)在“探究恒力做功与物体速度变化的关系”实验中,某实验小组采用如图甲所示的装置.实验步骤如下:
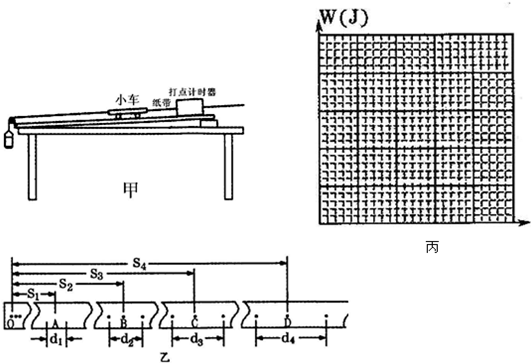
①把纸带的一端固定在小车的后面,另一端穿过打点计时器;
②改变木板的倾角,以重力的一个分力平衡小车及纸带受到的摩擦力;
③用细线将木板上的小车通过定滑轮与悬吊的砂桶相连(砂和桶总质量远小于小车总质量);
④接通电源,放开小车,让小车拖着纸带运动,打点计时器就在纸带上打下一系列的点;
⑤在纸带中选合适的点A、B、C、D…,测出它们到起点O的距离s1、s2、s3、s4…,并测出与它们相邻的两点间距离d1、d2、d3、d4…(如图乙),查得打点周期为T,将数据填入下表中;
⑥保持砂和桶质量不变,增加小车质量,重复实验步骤④、⑤,将数据填入下表中.
附表:小车第一次总质量M1=0.25kg,第二次总质量M2=0.5kg,T=0.02s
试问:
(1)判断重力的一个分力是否与小车及纸带受到的摩擦力平衡的直接证据是
(2)实验数据处理时,为什么探究功与v、v2、v3等的关系,而不是与
、
、
等的关系?
(3)将表格中的数据填写完整;
(4)比较表中第一次各组数据,得到的实验结论为:
(5)比较表中一、二两次数据,得到的实验结论为:
(6)请运用表中第二次数据在右图所示的坐标中作出相应的图象,验证理论的正确性(拉力用F表示).

①把纸带的一端固定在小车的后面,另一端穿过打点计时器;
②改变木板的倾角,以重力的一个分力平衡小车及纸带受到的摩擦力;
③用细线将木板上的小车通过定滑轮与悬吊的砂桶相连(砂和桶总质量远小于小车总质量);
④接通电源,放开小车,让小车拖着纸带运动,打点计时器就在纸带上打下一系列的点;
⑤在纸带中选合适的点A、B、C、D…,测出它们到起点O的距离s1、s2、s3、s4…,并测出与它们相邻的两点间距离d1、d2、d3、d4…(如图乙),查得打点周期为T,将数据填入下表中;
⑥保持砂和桶质量不变,增加小车质量,重复实验步骤④、⑤,将数据填入下表中.
附表:小车第一次总质量M1=0.25kg,第二次总质量M2=0.5kg,T=0.02s
| 物理量 数据 测量点 |
测量点到O 点的距离s (cm) |
测量点前后 两点间距离d (cm) |
小车获得 的速度v (m/s) |
小车获得速度的平方v2 [(m/s)2] |
小车获得速度的三次方v3 [(m/s)3] | |
| 第 一 次 |
A | 20.05 | 3.58 | 0.90 | 08.1 | 0.73 |
| B | 40.00 | 5.06 | 1.27 | 1.61 | 2.05 | |
| C | 60.15 | 6.20 | 1.55 | 2.40 | 3.72 | |
| D | 80.24 | 7.16 | ||||
| 第 二 次 |
A | 20.15 | 2.53 | 0.63 | 0.40 | 0.25 |
| B | 40.10 | 3.58 | 0.90 | 0.81 | 0.73 | |
| C | 59.90 | 4.38 | 1.10 | 1.21 | 1.33 | |
| D | 81.20 | 5.06 | 1.27 | 1.61 | 2.05 | |
(1)判断重力的一个分力是否与小车及纸带受到的摩擦力平衡的直接证据是
纸带上点迹间距相等
纸带上点迹间距相等
;(2)实验数据处理时,为什么探究功与v、v2、v3等的关系,而不是与
| 1 |
| v |
| 1 |
| v2 |
| 1 |
| v3 |
速度随做功的增加而增加
速度随做功的增加而增加
;(3)将表格中的数据填写完整;
(4)比较表中第一次各组数据,得到的实验结论为:
W∝v2
W∝v2
;(5)比较表中一、二两次数据,得到的实验结论为:
W∝Mv2
W∝Mv2
;(6)请运用表中第二次数据在右图所示的坐标中作出相应的图象,验证理论的正确性(拉力用F表示).
分析:(1)若重力分力与小车及纸带受到的摩擦力平衡,则小车做匀速运动,纸带点迹间隔应该相等.
(2)因为得到的数据显示速度随做功的增加而增加,故不必考虑反比关系.
(3)由平均速度等于中间时刻的瞬时速度,可得测量点D的速度,进而得到速度平方.
(4)由数据可以看出,位移与速度平方成正比,而功W=Fs.
(5)比较表中一、二两次数据,可以看出功与质量也成正比.
(6)由给定的数据可得图象.
(2)因为得到的数据显示速度随做功的增加而增加,故不必考虑反比关系.
(3)由平均速度等于中间时刻的瞬时速度,可得测量点D的速度,进而得到速度平方.
(4)由数据可以看出,位移与速度平方成正比,而功W=Fs.
(5)比较表中一、二两次数据,可以看出功与质量也成正比.
(6)由给定的数据可得图象.
解答:解:
(1)正好平衡掉摩擦力的判定依据是:若分力与小车及纸带受到的摩擦力平衡,小车做匀速运动,纸带点迹间隔应该相等.
(2)因为得到的数据显示速度随做功的增加而增加,故我们只考虑正比关系,而不必考虑反比关系.
(3)由平均速度等于中间时刻的瞬时速度,可得测量点D的速度:vD=
m/s=1.79m/s,速度平方为:vD2=1.792m2/s2=3.20m2/s2
(4)由数据可以看出,位移与速度平方成正比,又功W=Fs,故可知功与速度平方成正比,即:W∝v2.
(5)比较表中一、二两次数据,可以看出功与质量也成正比,故综合(4)的结论可知:W∝Mv2;
(6)由表格中的第二次数据,建立纵轴为功,横轴为速度平方,描点作图如图:
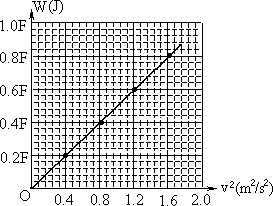
故答案为(1)纸带上点迹间距相等;
(2)速度随做功的增加而增加;
(3)1.79,3.20;
(4)W∝v2;
(5)W∝Mv2;
(6)如上图所示.
(1)正好平衡掉摩擦力的判定依据是:若分力与小车及纸带受到的摩擦力平衡,小车做匀速运动,纸带点迹间隔应该相等.
(2)因为得到的数据显示速度随做功的增加而增加,故我们只考虑正比关系,而不必考虑反比关系.
(3)由平均速度等于中间时刻的瞬时速度,可得测量点D的速度:vD=
| 7.16×10-2 |
| 0.04 |
(4)由数据可以看出,位移与速度平方成正比,又功W=Fs,故可知功与速度平方成正比,即:W∝v2.
(5)比较表中一、二两次数据,可以看出功与质量也成正比,故综合(4)的结论可知:W∝Mv2;
(6)由表格中的第二次数据,建立纵轴为功,横轴为速度平方,描点作图如图:

故答案为(1)纸带上点迹间距相等;
(2)速度随做功的增加而增加;
(3)1.79,3.20;
(4)W∝v2;
(5)W∝Mv2;
(6)如上图所示.
点评:本题题目看着挺大,实际都是比较简单的,知道如何算是正好平衡掉摩擦力,掌握基本的功与速度的关系,可以解答本题,属于基础题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2009?巢湖一模)如图所示,在水平传送带上有三个质量分别为m1、m2、m3的木块1、2、3,中间分别用一原长为L、劲度系数为k的轻弹簧连接起来,木块与传送带间的动摩擦因数为μ,现用水平细绳将木块1固定在左边的墙上,传送带按图示方向匀速运动,当三个木块达到平衡后,2、3两木块之间的距离是( )
(2009?巢湖一模)如图所示,在水平传送带上有三个质量分别为m1、m2、m3的木块1、2、3,中间分别用一原长为L、劲度系数为k的轻弹簧连接起来,木块与传送带间的动摩擦因数为μ,现用水平细绳将木块1固定在左边的墙上,传送带按图示方向匀速运动,当三个木块达到平衡后,2、3两木块之间的距离是( ) (2009?巢湖一模)如图所示,在光滑的水平面上,质量为M=3.0kg的长木板A的左端叠放着一个质量为m=1.0kg的小物块B(可视为质点),处于静止状态,小物块与木板之间的动摩擦因数μ=0.30.在木板A的左端正上方,用长为R=0.80m不可伸长的轻绳将质量为m=1.0kg的小球C悬于固定点O,现将轻绳拉直使小球C于O点以下与水平方向成θ=30°角的位置(如图所示),由静止释放.此后,小球C与B恰好发生正碰且无机械能损失.空气阻力不计,取g=10m/s2.求:
(2009?巢湖一模)如图所示,在光滑的水平面上,质量为M=3.0kg的长木板A的左端叠放着一个质量为m=1.0kg的小物块B(可视为质点),处于静止状态,小物块与木板之间的动摩擦因数μ=0.30.在木板A的左端正上方,用长为R=0.80m不可伸长的轻绳将质量为m=1.0kg的小球C悬于固定点O,现将轻绳拉直使小球C于O点以下与水平方向成θ=30°角的位置(如图所示),由静止释放.此后,小球C与B恰好发生正碰且无机械能损失.空气阻力不计,取g=10m/s2.求: (2009?巢湖一模)空气中的负离子对人的健康极为有益.人工产生负氧离子的方法最常见的是电晕放电法.如图所示,一排针状负极和环形正极之间加上直流高压电,电压达5000V左右,使空气发生电离,从而产生负氧离子(O3-)排出,使空气清新化,针状负极与环形正极间距为5mm,且视为匀强电场,电场强度为E,电场对负氧离子的作用力为F,则( )
(2009?巢湖一模)空气中的负离子对人的健康极为有益.人工产生负氧离子的方法最常见的是电晕放电法.如图所示,一排针状负极和环形正极之间加上直流高压电,电压达5000V左右,使空气发生电离,从而产生负氧离子(O3-)排出,使空气清新化,针状负极与环形正极间距为5mm,且视为匀强电场,电场强度为E,电场对负氧离子的作用力为F,则( ) (2009?巢湖一模)如图所示,一个均匀的带电圆环,带电量为+Q,半径为R,放在绝缘水平桌面上.圆心为O点,过O点做一竖直线,在此线上取一点A,使A到O点的距离为R,在A点放一检验电荷+q,则+q在A点所受的电场力为( )
(2009?巢湖一模)如图所示,一个均匀的带电圆环,带电量为+Q,半径为R,放在绝缘水平桌面上.圆心为O点,过O点做一竖直线,在此线上取一点A,使A到O点的距离为R,在A点放一检验电荷+q,则+q在A点所受的电场力为( ) (2009?巢湖一模)如图所示,A、B分别为竖直光滑圆轨道的最低点和最高点.已知小球通过A点的速度
(2009?巢湖一模)如图所示,A、B分别为竖直光滑圆轨道的最低点和最高点.已知小球通过A点的速度