题目内容
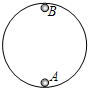（2009?巢湖一模）如图所示，A、B分别为竖直光滑圆轨道的最低点和最高点．已知小球通过A点的速度υ=2| 5 |
| 5 |
分析：本题中，小球从圆周内轨道的最高点运动到最低点过程，只有重力做功，可根据动能定理或机械能守恒定律列式，同时小球能通过最高点的情况为在最高点时m
≤G．
| v2 |
| r |
解答：解：小球由A至B过程中，由动能定理，得到：
mvB2+2mgr=
mvA2；
解得，vB=
=
；
小球在最高点，F+G=m
≥G；
由以上两式得到：r≤0.4m，v≥
=2m/s；
本题选错误的，故选D．
| 1 |
| 2 |
| 1 |
| 2 |
解得，vB=
|
| 20-40r |
小球在最高点，F+G=m
| v2 |
| r |
由以上两式得到：r≤0.4m，v≥
| gr |
本题选错误的，故选D．
点评：球在圆周内轨道内部运动，与用绳子系球在竖直面运动，受力与运动情况相同，可简化为同一种物理模型；要注意球能通过最高点的条件为v≥
；
| gr |
练习册系列答案
百年学典课时学练测系列答案
相关题目
（2009?巢湖一模）如图所示，在水平传送带上有三个质量分别为m1、m2、m3的木块1、2、3，中间分别用一原长为L、劲度系数为k的轻弹簧连接起来，木块与传送带间的动摩擦因数为μ，现用水平细绳将木块1固定在左边的墙上，传送带按图示方向匀速运动，当三个木块达到平衡后，2、3两木块之间的距离是（ ）
（2009?巢湖一模）如图所示，在光滑的水平面上，质量为M=3.0kg的长木板A的左端叠放着一个质量为m=1.0kg的小物块B（可视为质点），处于静止状态，小物块与木板之间的动摩擦因数μ=0.30．在木板A的左端正上方，用长为R=0.80m不可伸长的轻绳将质量为m=1.0kg的小球C悬于固定点O，现将轻绳拉直使小球C于O点以下与水平方向成θ=30°角的位置（如图所示），由静止释放．此后，小球C与B恰好发生正碰且无机械能损失．空气阻力不计，取g=10m/s2．求：
（2009?巢湖一模）空气中的负离子对人的健康极为有益．人工产生负氧离子的方法最常见的是电晕放电法．如图所示，一排针状负极和环形正极之间加上直流高压电，电压达5000V左右，使空气发生电离，从而产生负氧离子（O3-）排出，使空气清新化，针状负极与环形正极间距为5mm，且视为匀强电场，电场强度为E，电场对负氧离子的作用力为F，则（ ）
（2009?巢湖一模）如图所示，一个均匀的带电圆环，带电量为+Q，半径为R，放在绝缘水平桌面上．圆心为O点，过O点做一竖直线，在此线上取一点A，使A到O点的距离为R，在A点放一检验电荷+q，则+q在A点所受的电场力为（ ）