题目内容
（2009?巢湖一模）如图所示，在水平传送带上有三个质量分别为m1、m2、m3的木块1、2、3，中间分别用一原长为L、劲度系数为k的轻弹簧连接起来，木块与传送带间的动摩擦因数为μ，现用水平细绳将木块1固定在左边的墙上，传送带按图示方向匀速运动，当三个木块达到平衡后，2、3两木块之间的距离是（ ）分析：当三木块达到平衡状态后，三个木块的合力都为零．对木块3研究，由平衡条件和胡克定律求出2和3间弹簧伸长量．
解答：解：当三木块达到平衡状态后，对木块3进行受力分析，可知2和3间弹簧的弹力等于木块3所受的滑动摩擦力，即：
μm3g=kx3，解得2和3间弹簧伸长量为：x3=
；
所以23间的距离为L+
；
故选：C．
μm3g=kx3，解得2和3间弹簧伸长量为：x3=
| μm3g |
| k |
所以23间的距离为L+
| μm3g |
| k |
故选：C．
点评：本题涉及三个物体的平衡问题，首先要灵活选择研究对象，分析受力情况，由平衡条件和胡克定律求出两个弹簧的伸长量
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
（2009?巢湖一模）如图所示，在光滑的水平面上，质量为M=3.0kg的长木板A的左端叠放着一个质量为m=1.0kg的小物块B（可视为质点），处于静止状态，小物块与木板之间的动摩擦因数μ=0.30．在木板A的左端正上方，用长为R=0.80m不可伸长的轻绳将质量为m=1.0kg的小球C悬于固定点O，现将轻绳拉直使小球C于O点以下与水平方向成θ=30°角的位置（如图所示），由静止释放．此后，小球C与B恰好发生正碰且无机械能损失．空气阻力不计，取g=10m/s2．求：
（2009?巢湖一模）空气中的负离子对人的健康极为有益．人工产生负氧离子的方法最常见的是电晕放电法．如图所示，一排针状负极和环形正极之间加上直流高压电，电压达5000V左右，使空气发生电离，从而产生负氧离子（O3-）排出，使空气清新化，针状负极与环形正极间距为5mm，且视为匀强电场，电场强度为E，电场对负氧离子的作用力为F，则（ ）
（2009?巢湖一模）如图所示，一个均匀的带电圆环，带电量为+Q，半径为R，放在绝缘水平桌面上．圆心为O点，过O点做一竖直线，在此线上取一点A，使A到O点的距离为R，在A点放一检验电荷+q，则+q在A点所受的电场力为（ ）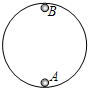
（2009?巢湖一模）如图所示，A、B分别为竖直光滑圆轨道的最低点和最高点．已知小球通过A点的速度