��Ŀ����
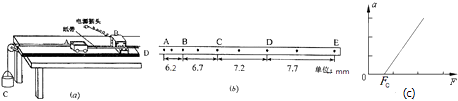
����Ŀ����ͼ��ʾ��һ����Ϊm=0.016kg����L=0.5m����d=0.1m������R=0.1���ľ�����Ȧ����h1=5m�ĸߴ��ɾ�ֹ��ʼ���䣬Ȼ�������ǿ�ų������±߽���ų�ʱ�����ڴų��������ã���Ȧ�����������˶���
��1������ǿ�ų��ĴŸ�Ӧǿ��B��
��2�������Ȧ���±�ͨ���ų���������ʱ��t=0.15s����ų�����ĸ߶�h2 ��
��3������Ȧ���±߸��뿪�ų���˲�䣬��Ȧ�ļ��ٶȵĴ�С�ͷ���
��4������Ȧ���±߽���ų���ʼ����Ȧ�±��뿪�ų���ʱ���ڣ�����Ȧ�в����Ľ������Ƕ��٣�
���𰸡�
��1��
�⣺��Ȧ�����������˶�����е���غ㣬�ɻ�е���غ㶨�ɵã�mgh1= ![]() mv02��
mv02��
��Ȧ����ų�ʱ�ܵ��İ�������F=BId= ![]() ��
��
��Ȧ����ų�ʱ������ֱ���˶�����ƽ�������ã�mg= ![]() ��
��
�������ݽ�ã�B=0.4T
��2��
�⣺��Ȧ�±߽���ų������������˶���������ֱ���˶���ʱ�䣺t0= ![]() ��
��
�������ݽ�ã�t0=0.05s��
��Ȧ�������˶���ʱ��Ϊ��t1=t��t0=0.1s��
λ�ƣ�h2=L+v0t1+ ![]() gt12��
gt12��
�������ݽ�ã�h2=1.55m
��3��
�⣺��Ȧ�±߸��뿪�ų�˲�䣬��Ȧ�ܵ���v=v0+gt1��
�������ݽ�ã�v=11m/s��
��ţ�ٵڶ����ɵã� ![]() ��mg=ma��
��mg=ma��
�������ݽ�ã�a=1m/s2����������
��4��
�⣺��Ȧ����������ת��Ϊ�����ȣ�
Q=mgL=0.016��10��0.5=0.08J
����������1���ɻ�е���غ㶨�������Ȧ����ų�ʱ���ٶȣ�Ȼ����ƽ����������Ÿ�Ӧǿ�ȣ���2������߿����ٽ���ų����̵�ʱ�䣬Ȼ������߿��������˶���ʱ�䣬Ȼ������ų��Ŀ��ȣ���3�������Ȧ�±��뿪�ų�ʱ���ٶȣ�Ȼ����ţ�ٵڶ�����������ٶȣ���4����Ȧ����������ת��Ϊ�����ȣ�
�����㾫�������ôŸ�Ӧǿ�Ⱥͽ������ɶ���Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪�Ÿ�Ӧǿ����ʸ�����ų���ij��ĴŸ�Ӧǿ�ȵķ�����Ǹõ�Ĵų�����ͨ���õ�ĴŸ��ߵ����߷���������:Q=I2Rt��ʽ��Q��ʾ����ͨ�������������������λ��J.�������������ǶԴ������·���ǶԷǴ������·�������õģ�

 ϰ�⾫ѡϵ�д�
ϰ�⾫ѡϵ�д�����Ŀ���ƺ��ʻ�ᵼ�����లȫ����������Ϊ��ʻԱ�ķ�Ӧʱ��䳤����Ӧʱ����ָ��ʻԱ�ӷ����������ȡ�ƶ���ʱ�䣮�±�����˼����������ָ��ʻԱ�ӷ����������ȡ�ƶ���ʱ����������ʻ�ľ��룬���ƶ���������ָ��ʻԱ�ӷ������������ֹͣ��ʻ�ľ��루���������ƶ�ʱ�ļ��ٶȴ�С����ͬ����
�ٶ�/��ms��1�� | ˼������/m | �ƶ�����/m | ||
���� | �ƺ� | ���� | �ƺ� | |
15 | 7.5 | 15.0 | 22.5 | 30.0 |
20 | 10.0 | 20.0 | 36.7 | 46.7 |
25 | 12.5 | 25.0 | 54.2 | 66.7 |
�����ϱ���֪������˵����ȷ���ǣ�������
A. ��ʻԱ��������·�Ӧʱ��Ϊ0.5 s
B. ��ʻԱ�ƺ�Ӧʱ�����������¶�0.5 s
C. ��ʻԱ��ȡ�ƶ���ʩ�������ļ��ٶȴ�СΪ3.75 m/s2
D. ��������25 m/s���ٶ���ʻʱ������ǰ��60 m�������飬�ƺ��ʻ���ܰ�ȫͣ��