题目内容
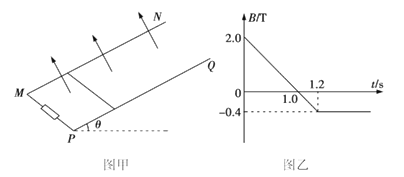
【题目】将两足够长的平行直导轨MN、PQ固定在绝缘斜面上,已知导轨与水平面之间的夹角为θ=30°,两导轨之间的距离为L=2 m,下端接有R=1.5 Ω的定值电阻,如图甲所示。在整个空间加一范围足够大且方向垂直导轨平面的匀强磁场,磁场的磁感应强度大小随时间的变化规律如图乙所示,t=0时磁感应强度的方向垂直导轨平面向上。将一质量为m=1.4 kg、阻值为r=0.5 Ω、长度为L=2 m的导体棒垂直地放在导轨上且与导轨始终接触良好,开始时导体棒与MP的距离为L1=1 m,其他电阻不计,已知导体棒与导轨之间的动摩擦因数为μ=![]() ,最大静摩擦力等于滑动摩擦力,重力加速度g=10 m/s2。
,最大静摩擦力等于滑动摩擦力,重力加速度g=10 m/s2。
(1)如果导体棒在0~1 s内始终不动,求流过定值电阻的电流大小以及方向;
(2)分析t=1.1 s时导体棒所处的状态以及此时所受摩擦力的大小和方向;
(3)如果t=1.2 s时在导体棒上加一沿导轨向上的外力F,使导体棒沿导轨向上以a=5 m/s2的加速度做匀加速直线运动,写出该外力随时间变化的表达式。
【答案】(1)I=![]() =2 A;电流方向为M→P(2)导体棒受到的摩擦力f =7.8 N,方向沿斜面向上(3)F=21.08+1.6t(N)(t≥1.2 s)
=2 A;电流方向为M→P(2)导体棒受到的摩擦力f =7.8 N,方向沿斜面向上(3)F=21.08+1.6t(N)(t≥1.2 s)
【解析】(1)由法拉第电磁感应定律,得![]()
由闭合电路欧姆定律,得![]()
由楞次定律得电流方向为M→P
(2)t=1.1s时,电流大小不变,则安培力![]() ,方向沿斜面向下
,方向沿斜面向下
导体棒与导轨之间的最大静摩擦力![]()
对导体棒受力分析,可知![]() ,导体棒仍保持静止
,导体棒仍保持静止
所以导体棒受到的摩擦力![]() ,方向沿斜面向上
,方向沿斜面向上
(3)1.2s后,由法拉第电磁感应定律得![]()
![]() ,
, ![]() ,
, ![]()
由牛顿第二定律得![]()
解得![]()

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目