题目内容
11. 靠在一起的M,N两转盘靠摩擦转动,两盘均绕过圆心的竖直轴转动,M盘的半径为r,N盘的半径R=2r,A为M盘边缘上的一点,B,C为N盘边缘上的两点,且B,C连线过圆心O,当O′,A,B,C在一条直线上时,从O′的正上方P点以初速度v0沿ABC方向水平抛出一小球.半径O′A与v0方向相同,如图所示,小球与圆盘碰撞后不再弹起,且恰好落在C点,重力加速度为g.则( )
靠在一起的M,N两转盘靠摩擦转动,两盘均绕过圆心的竖直轴转动,M盘的半径为r,N盘的半径R=2r,A为M盘边缘上的一点,B,C为N盘边缘上的两点,且B,C连线过圆心O,当O′,A,B,C在一条直线上时,从O′的正上方P点以初速度v0沿ABC方向水平抛出一小球.半径O′A与v0方向相同,如图所示,小球与圆盘碰撞后不再弹起,且恰好落在C点,重力加速度为g.则( )| A. | 若M盘转动角速度ω=$\frac{2π{v}_{0}}{r}$,则小球抛出时O′的高度为$\frac{g{r}^{2}}{2{v}_{0}^{2}}$ | |
| B. | 若小球抛出时到O′的高度为$\frac{g{r}^{2}}{2{v}_{0}^{2}}$,则当M盘转动时角速度必为ω=$\frac{2π{v}_{0}}{r}$ | |
| C. | 只要M盘转动角速度满足ω=$\frac{2nπ{v}_{0}}{5r}$(n∈N+),小球就可能落在C点 | |
| D. | 只要小球抛出时到O′的高度恰当,小球就可能落在C点 |
分析 根据平抛运动的规律知h=$\frac{1}{2}g{t}^{2}$,x=v0t,当t=$\frac{2nπ}{ω}$,则x=r+2R=3r,若t=$\frac{2nπ-π}{ω}$,则x=r,n=1、2、3…,然后逐项分析.
解答 解:A、根据平抛运动的规律知h=$\frac{1}{2}g{t}^{2}$,x=v0t,当t=$\frac{2nπ}{ω}$,则x=r+2R=3r,若t=$\frac{2nπ-π}{ω}$,则x=r,n=1、2、3…,即$\frac{2πn}{ω}=\frac{3r}{{v}_{0}}$或者$\frac{2nπ-π}{ω}$=$\frac{r}{{v}_{0}}$,若M盘转动角速度ω=$\frac{2π{v}_{0}}{r}$,则x=r,n=3,时间t=$\frac{r}{{v}_{0}}$,h=$\frac{1}{2}g{t}^{2}$=$\frac{1}{2}g•\frac{{r}^{2}}{{v}_{0}^{2}}$,故A正确;
B、根据A分析知,只要满足$\frac{2πn}{ω}=\frac{3r}{{v}_{0}}$(n=1、2、3…)即可,故B错误;
C、根据A分析知角速度满足ω=$\frac{2πn{v}_{0}}{3r}$(n=1、2、3…)或者ω=$\frac{2nπ-π}{r}•{v}_{0}$(n=1、2、3…),故C错误;
D、根据以上分析要想到达C点,除了考虑高度还与初速度有关,故D错误;
故选:A
点评 此题考查圆周运动与平抛运动的结合,注意时间关系和位移关系,C可能是转过半周也可能是一周.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案
相关题目
2. 如图,一只蚂蚁从A点出发,沿边长为a的正方形路线爬行,经过B、C、D后又回到A点,则在这一过程中( )
如图,一只蚂蚁从A点出发,沿边长为a的正方形路线爬行,经过B、C、D后又回到A点,则在这一过程中( )
 如图,一只蚂蚁从A点出发,沿边长为a的正方形路线爬行,经过B、C、D后又回到A点,则在这一过程中( )
如图,一只蚂蚁从A点出发,沿边长为a的正方形路线爬行,经过B、C、D后又回到A点,则在这一过程中( )| A. | 蚂蚁的位移大小为4a | B. | 蚂蚁的位移为零 | ||
| C. | 蚂蚁运动的路程为零 | D. | 蚂蚁运动的路程和位移都为零 |
6. 如图所示,28根通有同向等大电流的长直导线(彼此绝缘)正好紧密排列在以O为圆心的圆周上,直径BD水平,AC竖直,直导线中电流方向均垂直纸面向外,现将B处的长直导线撤走,而将C处的长直导线平移到圆心O处,则圆心O处的长直导线所受安培力的方向( )
如图所示,28根通有同向等大电流的长直导线(彼此绝缘)正好紧密排列在以O为圆心的圆周上,直径BD水平,AC竖直,直导线中电流方向均垂直纸面向外,现将B处的长直导线撤走,而将C处的长直导线平移到圆心O处,则圆心O处的长直导线所受安培力的方向( )
 如图所示,28根通有同向等大电流的长直导线(彼此绝缘)正好紧密排列在以O为圆心的圆周上,直径BD水平,AC竖直,直导线中电流方向均垂直纸面向外,现将B处的长直导线撤走,而将C处的长直导线平移到圆心O处,则圆心O处的长直导线所受安培力的方向( )
如图所示,28根通有同向等大电流的长直导线(彼此绝缘)正好紧密排列在以O为圆心的圆周上,直径BD水平,AC竖直,直导线中电流方向均垂直纸面向外,现将B处的长直导线撤走,而将C处的长直导线平移到圆心O处,则圆心O处的长直导线所受安培力的方向( )| A. | 沿∠COB的角平分线向下 | B. | 沿∠AOB的角平分线向上 | ||
| C. | 沿∠AOD的角平分线向上 | D. | 沿∠COD的角平分线向下 |
3.相对论认为,在不同参考系中测量同一过程的位移和时间,下列说法正确的是( )
| A. | 位移和时间均不同 | B. | 位移和时间均相同 | ||
| C. | 位移相同,时间不同 | D. | 位移不同,时间相同 |
2.质量是2000kg、额定功率为80kW的汽车,在平直公路上行驶中的最大速度为20m/s.若汽车从静止开始做匀加速直线运动,加速度大小为2m/s2,运动中的阻力不变则汽车做匀加速运动的时间为5 s.
3. 如图所示,四个相同的表头分别改装成两个安培表和两个伏特表.安培表A1的量程大于A2的量程,伏特表V1的量程大V2的量程,把它们按图接入电路,则( )
如图所示,四个相同的表头分别改装成两个安培表和两个伏特表.安培表A1的量程大于A2的量程,伏特表V1的量程大V2的量程,把它们按图接入电路,则( )
 如图所示,四个相同的表头分别改装成两个安培表和两个伏特表.安培表A1的量程大于A2的量程,伏特表V1的量程大V2的量程,把它们按图接入电路,则( )
如图所示,四个相同的表头分别改装成两个安培表和两个伏特表.安培表A1的量程大于A2的量程,伏特表V1的量程大V2的量程,把它们按图接入电路,则( )| A. | 安培表A1的读数大于安培表A2的读数 | |
| B. | 安培表A1的偏转角小于安培表A2的偏转角 | |
| C. | 伏特表V1的读数小于伏特表V2的读数 | |
| D. | 伏特表V1的偏转角等于伏特表V2的偏转角 |
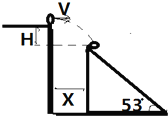 如图所示,一小球自平台上水平抛出,恰好落在平台前一倾角α=53°的斜面顶端,并刚好沿斜面下滑(此时速度方向沿斜面方向),已知斜面顶端与平台高度差h=0.8m,g=10m/s2,则小球水平抛出的初速度为3m/s,斜面与平台边缘的水平距离为1.2m.
如图所示,一小球自平台上水平抛出,恰好落在平台前一倾角α=53°的斜面顶端,并刚好沿斜面下滑(此时速度方向沿斜面方向),已知斜面顶端与平台高度差h=0.8m,g=10m/s2,则小球水平抛出的初速度为3m/s,斜面与平台边缘的水平距离为1.2m.
 充满一定质量的最理想气体的气缸A的底部左端与一两端开口,竖直放置的细玻璃管C连通(内装水银),气缸A内右侧有一带有手柄的活塞B,初始时,玻璃管C内两边水银面相平与气缸底部,水银面与C管底部高度差为h=12.5cm,活塞B距离气缸左端L=40cm,现缓缓向左推进活塞(不计活塞与气缸壁间的摩擦,在活塞向左推进过程中气缸不漏气),已知大气压等于p0=75cmHg=1.0×105Pa,活塞横截面积为S=40cm2,当玻璃管C右侧竖直管水银恰好全部被挤出时,求:
充满一定质量的最理想气体的气缸A的底部左端与一两端开口,竖直放置的细玻璃管C连通(内装水银),气缸A内右侧有一带有手柄的活塞B,初始时,玻璃管C内两边水银面相平与气缸底部,水银面与C管底部高度差为h=12.5cm,活塞B距离气缸左端L=40cm,现缓缓向左推进活塞(不计活塞与气缸壁间的摩擦,在活塞向左推进过程中气缸不漏气),已知大气压等于p0=75cmHg=1.0×105Pa,活塞横截面积为S=40cm2,当玻璃管C右侧竖直管水银恰好全部被挤出时,求: