题目内容
1．
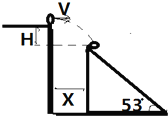如图所示，一小球自平台上水平抛出，恰好落在平台前一倾角α=53°的斜面顶端，并刚好沿斜面下滑（此时速度方向沿斜面方向），已知斜面顶端与平台高度差h=0.8m，g=10m/s2，则小球水平抛出的初速度为3m/s，斜面与平台边缘的水平距离为1.2m．
分析 由题意可知小球到达斜面时的速度方向，再由平抛运动的规律可求出小球的初速度；
水平距离为小球在空中运行时的水平位移，则由水产位移公式可求得斜面与平台边缘的水平距离．
解答 解：由题意可知：小球落到斜面上时速度方向沿向下，所以有
vy=v0tan53°
又vy2=2gh
代入数据，得vy=4m/s，v0=3m/s
故小球的水平速度为3m/s；
由vy=gt得 t=0.4s
斜面与平台边缘的水平距离 x=v0t1=3×0.4=1.2m
故答案为：3m/s，1.2m．
点评 本题的解题关键在于明确题干中“沿斜面下滑”的含义，从而明确小球落到斜面时的实际速度，由平抛运动的规律解答．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
某同学做了“测定玩具枪子弹与透明物块相互作用力”的实验，如图所示，将质量为m的子弹以速度v0沿水平方向射入固定在光滑水平面上质量为M的透明物块中，测得子弹射入的深度为d，设子弹与物块之间的相互作用力的大小与物块的运动状态无关．请你帮该同学计算：
9．有一宇宙飞船到了某行星上（该行星没有自转运动），以速度v接近行星赤道表面围绕行星做匀速圆周运动，测出运动的周期为T，已知引力常量为G，则可得（ ）
| A． | 该行星的半径为$\frac{πvT}{2}$ | B． | 该行星的平均密度为$\frac{3π}{G{T}^{2}}$ | ||
| C． | 无法测出该行星的质量 | D． | 该行星表面的重力加速度为$\frac{2v}{T}$ |
16．质量为m的汽车在平直公路上行驶，其功率恒为P，最大行驶速度为v1，当车速为v2时（v2＜v1），若阻力恒定，则汽车此时的加速度为（ ）
| A． | $\frac{P}{{m{v_2}}}$ | B． | $\frac{P}{{m（{{v_1}-{v_2}}）}}$ | C． | $\frac{{P（{{v_1}-{v_2}}）}}{{m{v_1}{v_2}}}$ | D． | $\frac{{P（{{v_1}+{v_2}}）}}{{m{v_1}{v_2}}}$ |
6．振动周期为T、振幅为A、位于x=0点的波源从平衡位置沿y轴正向开始做简谐运动．该波源产生的一维简谐横波沿x轴正向传播，波速为v，传播过程中无能量损失．一段时间后，该振动传播至某质点P，关于质点P振动的说法正确的是（ ）
| A． | 振幅一定为A | |
| B． | 速度的最大值一定为v | |
| C． | 开始振动的方向沿y轴向上或向下取决于它离波源的距离 | |
| D． | 若P点与波源距离s=vT，则质点P的位移与波源的相同 |
10．
如图所示，A、B两点高度差h=1m，质量m=1kg的物体从A点移动到B点的过程中，g取10m/s2，下列说法正确的是（ ）
如图所示，A、B两点高度差h=1m，质量m=1kg的物体从A点移动到B点的过程中，g取10m/s2，下列说法正确的是（ ）| A． | 重力做功10J | B． | 重力做功-10J | C． | 重力势能增加10J | D． | 重力势能减少10J |
11．
靠在一起的M，N两转盘靠摩擦转动，两盘均绕过圆心的竖直轴转动，M盘的半径为r，N盘的半径R=2r，A为M盘边缘上的一点，B，C为N盘边缘上的两点，且B，C连线过圆心O，当O′，A，B，C在一条直线上时，从O′的正上方P点以初速度v0沿ABC方向水平抛出一小球．半径O′A与v0方向相同，如图所示，小球与圆盘碰撞后不再弹起，且恰好落在C点，重力加速度为g．则（ ）
靠在一起的M，N两转盘靠摩擦转动，两盘均绕过圆心的竖直轴转动，M盘的半径为r，N盘的半径R=2r，A为M盘边缘上的一点，B，C为N盘边缘上的两点，且B，C连线过圆心O，当O′，A，B，C在一条直线上时，从O′的正上方P点以初速度v0沿ABC方向水平抛出一小球．半径O′A与v0方向相同，如图所示，小球与圆盘碰撞后不再弹起，且恰好落在C点，重力加速度为g．则（ ）| A． | 若M盘转动角速度ω=$\frac{2π{v}_{0}}{r}$，则小球抛出时O′的高度为$\frac{g{r}^{2}}{2{v}_{0}^{2}}$ | |
| B． | 若小球抛出时到O′的高度为$\frac{g{r}^{2}}{2{v}_{0}^{2}}$，则当M盘转动时角速度必为ω=$\frac{2π{v}_{0}}{r}$ | |
| C． | 只要M盘转动角速度满足ω=$\frac{2nπ{v}_{0}}{5r}$（n∈N+），小球就可能落在C点 | |
| D． | 只要小球抛出时到O′的高度恰当，小球就可能落在C点 |