题目内容
19.用如图1所示的实验装置验证机械能守恒定律.实验所用的电源为学生电源,输出电压为6V的交流电和直流电两种.重锤从高处由静止开始落下,重锤上拖着的纸带通过打点计时器打出一系列的点,对纸带上的点的痕迹进行测量,即可验证机械能守恒定律.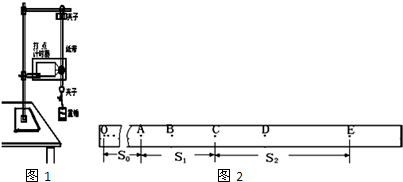
(1)下面列举了该实验的几个操作步骤:
A.按照图示的装置安装器件;
B.将打点计时器接到电源的直流输出端上;
C.用天平测量出重锤的质量;
D.释放悬挂纸带的夹子,同时接通电源开关打出一条纸带;
E.测量打出的纸带上某些点之间的距离;
F.根据测量的结果计算重锤下落过程中减少的重力势能在误差范围内是否等于增加的动能.
指出其中没有必要进行的或者操作不恰当的步骤,将其选项对应的字母填在右边的横线上BCD
(2)实验中得到一条纸带,如图2所示.根据打出的纸带,选取纸带上打出的连续五个点A、B、C、D、E,测出A点距起始点O的距离为s0,点A、C间的距离为s1,点C、E间的距离为s2,使用交流电的周期为T,设重锤质量为m,则ABC.
A.打点计时器打C点时重锤的动能为$\frac{m({s}_{1}+{s}_{2})^{2}}{32{T}^{2}}$
B.打点计时器在打O点和C点的这段时间内重锤的重力势能的减少量为mg(s0+s1)
C.重锤下落的加速度a的表达式为$\frac{{s}_{2}-{s}_{1}}{4{T}^{2}}$
D.重锤下落的加速度a的表达式为$\frac{{s}_{1}-{s}_{0}}{4{T}^{2}}$
(3)在本实验中发现,重锤减少的重力势能总是大于(填“大于”或“小于”)重锤增加的动能,其原因主要是因为在重锤下落过程中存在着阻力的作用,可以通过该实验装置测定该阻力的大小,试用(2)中已知物理量和纸带上的测量数据写出重锤在下落的过程中受到的平均阻力表达式为f=mg-m$\frac{{s}_{2}-{s}_{1}}{4{T}^{2}}$.
分析 解决实验问题首先要掌握该实验原理,了解实验的仪器、操作步骤和数据处理以及注意事项,只有理解了这些才能真正了解具体实验操作的含义.
本实验需要验证的是重力势能的减小量和动能的增加量是否相等,根据下落的高度求出重力势能的减小量,根据某段时间内的平均速度等于中间时刻的瞬时速度求出瞬时速度的大小,从而求出动能的增加量.
解答 解:(1)B:将打点计时器接到电源的“交流输出”上,故B错误.
C:因为我们是比较mgh、$\frac{1}{2}$mv2的大小关系,故m可约去比较,不需要用天平.故C没有必要
D:开始记录时,应先给打点计时器通电打点,然后再释放重锤,让它带着纸带一同落下,如果先放开纸带让重物下落,再接通打点计时时器的电源,由于重物运动较快,不利于数据的采集和处理,会对实验产生较大的误差.故D错误.
故选:BCD.
(2)A、匀变速直线运动中,时间中点的速度大小等于该过程中的平均速度大小,因此有:
vC=$\frac{{{S}_{1}+S}_{2}}{4T}$,
打点计时器打C点时重锤的动能为EkC=$\frac{1}{2}$m${v}_{C}^{2}$=$\frac{m({s}_{1}+{s}_{2})^{2}}{32{T}^{2}}$,故A正确;
B、打点计时器在打O点和C点的这段时间内重锤的重力势能的减少量为mg(s0+s1).故B正确;
C、根据匀变速直线运动的推论公式△x=aT2可以求出加速度的大小,
得:重锤下落的加速度a的表达式为a=$\frac{{s}_{2}-{s}_{1}}{4{T}^{2}}$.故C正确;
D、由于OA的时间间隔不是2T,所以重锤下落的加速度a的表达式不等于$\frac{{s}_{1}-{s}_{0}}{4{T}^{2}}$,故D错误;
故选:ABC.
(3)在本实验中发现,重锤减少的重力势能总是大于重锤增加的动能,其原因主要是因为在重锤下落过程中存在着阻力的作用
重锤下落过程中,受到重力和阻力作用,根据牛顿第二定律得:mg-F=ma
重锤在下落过程中受到的平均阻力的大小F=m(g-a)=mg-m$\frac{{s}_{2}-{s}_{1}}{4{T}^{2}}$,
故答案为:(1)BCD
(2)ABC
(3)大于;mg-m$\frac{{s}_{2}-{s}_{1}}{4{T}^{2}}$
点评 只有明确了实验原理以及实验的数据测量,才能明确各项实验操作的具体含义,要熟练应用物理基本规律,因此这点在平时训练中要重点加强.

| A. | 该行星的半径为$\frac{πvT}{2}$ | B. | 该行星的平均密度为$\frac{3π}{G{T}^{2}}$ | ||
| C. | 无法测出该行星的质量 | D. | 该行星表面的重力加速度为$\frac{2v}{T}$ |
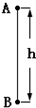 如图所示,A、B两点高度差h=1m,质量m=1kg的物体从A点移动到B点的过程中,g取10m/s2,下列说法正确的是( )
如图所示,A、B两点高度差h=1m,质量m=1kg的物体从A点移动到B点的过程中,g取10m/s2,下列说法正确的是( )| A. | 重力做功10J | B. | 重力做功-10J | C. | 重力势能增加10J | D. | 重力势能减少10J |
 在汽车无级变速器中,存在如图所示的装置,A是与B同轴相连的齿轮,C是与D同轴相连的齿轮,A、C、M为相互咬合的齿轮,B与D不咬合.已知齿轮A、C规格相同,半径为R,齿轮B、D规格也相同,半径为1.5R,齿轮M的半径为0.9R.当齿轮M如图方向转动时( )
在汽车无级变速器中,存在如图所示的装置,A是与B同轴相连的齿轮,C是与D同轴相连的齿轮,A、C、M为相互咬合的齿轮,B与D不咬合.已知齿轮A、C规格相同,半径为R,齿轮B、D规格也相同,半径为1.5R,齿轮M的半径为0.9R.当齿轮M如图方向转动时( )| A. | 齿轮D和齿轮B的转动方向相反 | |
| B. | 齿轮D和齿轮A的转动周期之比为1:1 | |
| C. | 齿轮M和齿轮C的角速度大小之比为9:10 | |
| D. | 齿轮M和齿轮B边缘某点的线速度大小之比为2:3 |
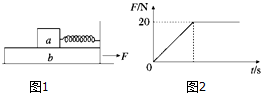
| A. | a与b始终保持相对静止 | |
| B. | a受到的摩擦力先减小、后增大再不变 | |
| C. | a受到的摩擦力先向左、后向右 | |
| D. | 当F=20N时,a受到的摩擦力为4N |
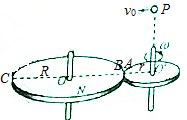 靠在一起的M,N两转盘靠摩擦转动,两盘均绕过圆心的竖直轴转动,M盘的半径为r,N盘的半径R=2r,A为M盘边缘上的一点,B,C为N盘边缘上的两点,且B,C连线过圆心O,当O′,A,B,C在一条直线上时,从O′的正上方P点以初速度v0沿ABC方向水平抛出一小球.半径O′A与v0方向相同,如图所示,小球与圆盘碰撞后不再弹起,且恰好落在C点,重力加速度为g.则( )
靠在一起的M,N两转盘靠摩擦转动,两盘均绕过圆心的竖直轴转动,M盘的半径为r,N盘的半径R=2r,A为M盘边缘上的一点,B,C为N盘边缘上的两点,且B,C连线过圆心O,当O′,A,B,C在一条直线上时,从O′的正上方P点以初速度v0沿ABC方向水平抛出一小球.半径O′A与v0方向相同,如图所示,小球与圆盘碰撞后不再弹起,且恰好落在C点,重力加速度为g.则( )| A. | 若M盘转动角速度ω=$\frac{2π{v}_{0}}{r}$,则小球抛出时O′的高度为$\frac{g{r}^{2}}{2{v}_{0}^{2}}$ | |
| B. | 若小球抛出时到O′的高度为$\frac{g{r}^{2}}{2{v}_{0}^{2}}$,则当M盘转动时角速度必为ω=$\frac{2π{v}_{0}}{r}$ | |
| C. | 只要M盘转动角速度满足ω=$\frac{2nπ{v}_{0}}{5r}$(n∈N+),小球就可能落在C点 | |
| D. | 只要小球抛出时到O′的高度恰当,小球就可能落在C点 |
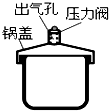 如图为某压力锅的结构简图.将压力阀套在出气孔上,给压力锅加热,在气体把压力阀顶起之前,锅内气体 ( )
如图为某压力锅的结构简图.将压力阀套在出气孔上,给压力锅加热,在气体把压力阀顶起之前,锅内气体 ( )| A. | 压强增大 | B. | 内能不变 | ||
| C. | 对外界做正功 | D. | 分子平均动能增大 | ||
| E. | 对外没有做功 |
 如图所示,水平传送带以2m/s的速度运行时,将一质量为2kg的工件轻轻放在传送带上(设传送带速度不变),工件与传送带之间的动摩擦因数为0.2,则放手后工件在3s内的位移是多少?摩擦力对工件做功为多少?(g取10m/s2)
如图所示,水平传送带以2m/s的速度运行时,将一质量为2kg的工件轻轻放在传送带上(设传送带速度不变),工件与传送带之间的动摩擦因数为0.2,则放手后工件在3s内的位移是多少?摩擦力对工件做功为多少?(g取10m/s2)