题目内容
2.质量是2000kg、额定功率为80kW的汽车,在平直公路上行驶中的最大速度为20m/s.若汽车从静止开始做匀加速直线运动,加速度大小为2m/s2,运动中的阻力不变则汽车做匀加速运动的时间为5 s.分析 当牵引力等于阻力时,速度最大,根据P=Fvm=fvm求出汽车所受的阻力.当匀加速运动速度达到最大时,功率达到额定功率,根据牛顿第二定律求出匀加速直线运动的牵引力,从而得出匀加速直线运动的最大速度,根据匀变速直线运动的速度时间公式求出匀加速运动的时间
解答 解:当牵引力等于阻力时,速度最大,由P=FV得:f=$\frac{P}{{v}_{m}}$=$\frac{80000}{20}$N=4×103N,
由F-f=ma 得:F=f+ma=4×103+2×103×2N=8×103N,
由P=FV得:V=$\frac{P}{F}$=$\frac{80000}{8×1{0}^{3}}$m/s=10m/s,
所以匀加速运动的时间为:t=$\frac{v}{a}$=$\frac{10}{2}$s=5s,
故答案为:5s
点评 解决本题的关键知道当牵引力等于阻力时,速度最大,最终做匀速直线运动,匀加速运动的末速度不是最大速度.

练习册系列答案
相关题目
10. 如图所示,A、B两点高度差h=1m,质量m=1kg的物体从A点移动到B点的过程中,g取10m/s2,下列说法正确的是( )
如图所示,A、B两点高度差h=1m,质量m=1kg的物体从A点移动到B点的过程中,g取10m/s2,下列说法正确的是( )
 如图所示,A、B两点高度差h=1m,质量m=1kg的物体从A点移动到B点的过程中,g取10m/s2,下列说法正确的是( )
如图所示,A、B两点高度差h=1m,质量m=1kg的物体从A点移动到B点的过程中,g取10m/s2,下列说法正确的是( )| A. | 重力做功10J | B. | 重力做功-10J | C. | 重力势能增加10J | D. | 重力势能减少10J |
11.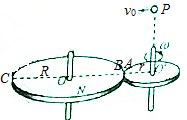 靠在一起的M,N两转盘靠摩擦转动,两盘均绕过圆心的竖直轴转动,M盘的半径为r,N盘的半径R=2r,A为M盘边缘上的一点,B,C为N盘边缘上的两点,且B,C连线过圆心O,当O′,A,B,C在一条直线上时,从O′的正上方P点以初速度v0沿ABC方向水平抛出一小球.半径O′A与v0方向相同,如图所示,小球与圆盘碰撞后不再弹起,且恰好落在C点,重力加速度为g.则( )
靠在一起的M,N两转盘靠摩擦转动,两盘均绕过圆心的竖直轴转动,M盘的半径为r,N盘的半径R=2r,A为M盘边缘上的一点,B,C为N盘边缘上的两点,且B,C连线过圆心O,当O′,A,B,C在一条直线上时,从O′的正上方P点以初速度v0沿ABC方向水平抛出一小球.半径O′A与v0方向相同,如图所示,小球与圆盘碰撞后不再弹起,且恰好落在C点,重力加速度为g.则( )
 靠在一起的M,N两转盘靠摩擦转动,两盘均绕过圆心的竖直轴转动,M盘的半径为r,N盘的半径R=2r,A为M盘边缘上的一点,B,C为N盘边缘上的两点,且B,C连线过圆心O,当O′,A,B,C在一条直线上时,从O′的正上方P点以初速度v0沿ABC方向水平抛出一小球.半径O′A与v0方向相同,如图所示,小球与圆盘碰撞后不再弹起,且恰好落在C点,重力加速度为g.则( )
靠在一起的M,N两转盘靠摩擦转动,两盘均绕过圆心的竖直轴转动,M盘的半径为r,N盘的半径R=2r,A为M盘边缘上的一点,B,C为N盘边缘上的两点,且B,C连线过圆心O,当O′,A,B,C在一条直线上时,从O′的正上方P点以初速度v0沿ABC方向水平抛出一小球.半径O′A与v0方向相同,如图所示,小球与圆盘碰撞后不再弹起,且恰好落在C点,重力加速度为g.则( )| A. | 若M盘转动角速度ω=$\frac{2π{v}_{0}}{r}$,则小球抛出时O′的高度为$\frac{g{r}^{2}}{2{v}_{0}^{2}}$ | |
| B. | 若小球抛出时到O′的高度为$\frac{g{r}^{2}}{2{v}_{0}^{2}}$,则当M盘转动时角速度必为ω=$\frac{2π{v}_{0}}{r}$ | |
| C. | 只要M盘转动角速度满足ω=$\frac{2nπ{v}_{0}}{5r}$(n∈N+),小球就可能落在C点 | |
| D. | 只要小球抛出时到O′的高度恰当,小球就可能落在C点 |
11.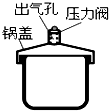 如图为某压力锅的结构简图.将压力阀套在出气孔上,给压力锅加热,在气体把压力阀顶起之前,锅内气体 ( )
如图为某压力锅的结构简图.将压力阀套在出气孔上,给压力锅加热,在气体把压力阀顶起之前,锅内气体 ( )
 如图为某压力锅的结构简图.将压力阀套在出气孔上,给压力锅加热,在气体把压力阀顶起之前,锅内气体 ( )
如图为某压力锅的结构简图.将压力阀套在出气孔上,给压力锅加热,在气体把压力阀顶起之前,锅内气体 ( )| A. | 压强增大 | B. | 内能不变 | ||
| C. | 对外界做正功 | D. | 分子平均动能增大 | ||
| E. | 对外没有做功 |
12.如图所示是行星m绕恒星M运动情况的示意图,则下列说法正确的是( )
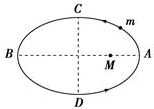

| A. | 速度最大点是A点 | B. | 速度最小点是C点 | ||
| C. | m从A 到B做加速运动 | D. | m从B 到A做加速运动 |
 如图所示,水平传送带以2m/s的速度运行时,将一质量为2kg的工件轻轻放在传送带上(设传送带速度不变),工件与传送带之间的动摩擦因数为0.2,则放手后工件在3s内的位移是多少?摩擦力对工件做功为多少?(g取10m/s2)
如图所示,水平传送带以2m/s的速度运行时,将一质量为2kg的工件轻轻放在传送带上(设传送带速度不变),工件与传送带之间的动摩擦因数为0.2,则放手后工件在3s内的位移是多少?摩擦力对工件做功为多少?(g取10m/s2)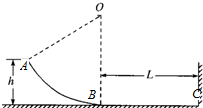 如图所示高度h=0.6m的光滑圆弧形轨道AB在B点与长为L=1.2m的水平粗糙轨道BC相切,在C点固定一竖直挡板,质量m=1kg的小球从A点由静止滑下,小球沿轨道ABC运动并与挡板发生碰撞,已知∠AOB=60°,圆心为O,取g=10m/s2.求:
如图所示高度h=0.6m的光滑圆弧形轨道AB在B点与长为L=1.2m的水平粗糙轨道BC相切,在C点固定一竖直挡板,质量m=1kg的小球从A点由静止滑下,小球沿轨道ABC运动并与挡板发生碰撞,已知∠AOB=60°,圆心为O,取g=10m/s2.求: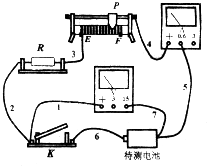 一节电动势约为9V、内阻约为2Ω的电池,允许通过的最大电流是500mA.为了测定该电池的电动势和内阻,选用了总阻值为50Ω的滑动变阻器以及电流表和电压表等,连成了如图所示的电路.
一节电动势约为9V、内阻约为2Ω的电池,允许通过的最大电流是500mA.为了测定该电池的电动势和内阻,选用了总阻值为50Ω的滑动变阻器以及电流表和电压表等,连成了如图所示的电路.