题目内容
【题目】某校兴趣小组制作了一个游戏装置，其简化模型如图所示，在 A 点用一弹射装置可 将静止的小滑块以 v0水平速度弹射出去，沿水平直线轨道运动到 B 点后，进入半径 R=0.3m的光滑竖直圆形轨道，运行一周后自 B 点向 C 点运动，C 点右侧有一陷阱，C、D 两点的竖 直高度差 h=0.2m，水平距离 s=0.6m，水平轨道 AB 长为 L1=1m，BC 长为 L2 =2.6m，小滑块与 水平轨道间的动摩擦因数 μ=0.5，重力加速度 g=10m/s2.
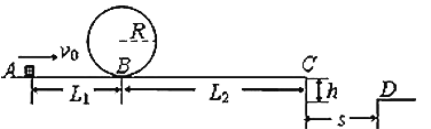
(1)若小滑块恰能通过圆形轨道的最高点，求小滑块在 A 点弹射出的速度大小；
(2)若游戏规则为小滑块沿着圆形轨道运行一周离开圆形轨道后只要不掉进陷阱即为胜出，求小滑块在 A 点弹射出的速度大小的范围。
【答案】（1）
（2）5m/s≤vA≤6m/s和vA≥
【解析】（1）小滑块恰能通过圆轨道最高点的速度为v，由牛顿第二定律： 
①
从B到最高点小滑块机械能守恒有： 
②
从A到B由动能定理得： 
③
由以上三式解得A点的速度为： 
（2）若小滑块刚好停在C处，从A到C由动能定理得： 
④
解得A点的速度为: 
若小滑块停在BC段，应满足
若小滑块能通过C点并恰好越过陷阱，利用平抛运动则有：
竖直方向：
⑤
水平方向： 
⑥
从A到C由动能定理得： 
⑦
解得： 
所以初速度的范围为： 
和
【题目】某实验小组想描绘标有“4V2W”的小灯泡的
图像,除导线和开关外还备有以下器材可供选择:
A.电流表
(量程0.6
,内阻约为1
)
B.电流表
(量程3.0A,内阻约为0.2
)
C.电压表
(量程5.0V,内阻约为5k
)
D.电压表
(量程15.0V,内阻约为15
)
E.滑动变阻器
(最大阻值为5
,额定电流500
)
F.滑动变阻器
(最大阻值为10
,额定电流2.0A)
G.电源(电动势为6.0V,内阻约为0.5
)
(1)实验中所用的电流表应选________;电压表应选________;滑动变阻器应选________.
(2)在虚线框内画出实验的电路图___________。
(3)经过正确的操作,测得的数据如下表,请根据下表数据在下方坐标系中描点画出小灯泡的曲线_________。
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
| 0 | 0.40 | 0.80 | 1.20 | 1.60 | 2.00 | 2.40 | 2.80 | 3.20 | 3.60 | 4.00 |
| 0 | 0.12 | 0.22 | 0.30 | 0.36 | 0.40 | 0.43 | 0.46 | 0.48 | 0.49 | 0.50 |
