��Ŀ����
17�� ��ͼ��ʾ����Ե����ϸ��һ������O�㣬��һ��ϵһ����Ϊm���������Ϊq��С��С��ֹʱ����O'�㣮�ֽ���װ�÷���ˮƽ���ҵ���ǿ�糡�У�С��ɾ�ֹ��A�㣬С��ֹʱϸ������ֱ����ɦȽǣ����������ٶ�Ϊg����
��ͼ��ʾ����Ե����ϸ��һ������O�㣬��һ��ϵһ����Ϊm���������Ϊq��С��С��ֹʱ����O'�㣮�ֽ���װ�÷���ˮƽ���ҵ���ǿ�糡�У�С��ɾ�ֹ��A�㣬С��ֹʱϸ������ֱ����ɦȽǣ����������ٶ�Ϊg������1��С������ֵ�ɣ��糡ǿ�ȵĴ�С��
��2����С����A�㾲ֹʱ������ϸ�߲���ʼ��ʱ����ʱ��t��С��糡�е�B�㣨ͼ��δ����B�㣬��С��һֱ�ڵ糡���˶���������AB����ĵ��Ʋ�UAB��С������ܵı仯��
���� ��1����С������������������ݹ�����ƽ�������͵糡����ʽF=qE���з�����⼴�ɣ�
��2�������������Ӷȣ�ȷ��λ���� UAB=Edcos��ȷ��UAB��С������ܵı仯��
��� 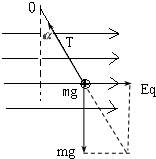 �⣺��1����С�����������������ͼ��ʾ������������糡������ͬ����Ϊ���磮
�⣺��1����С�����������������ͼ��ʾ������������糡������ͬ����Ϊ���磮
�������������ݹ�����ƽ���������ɵã�qE=mgtan�� ��$E=\frac{mgtan��}{q}$
��������2������ϸ�ߣ�a=$\frac{mgtan��}{qm}$=$\frac{gtan��}{q}$
tʱ��λ��Ϊd=$\frac{1}{2}a{t}^{2}$=$\frac{1}{2}\frac{{g}^{2}ta{n}^{2}��}{{q}^{2}}$
UAB=Edcos�ȨT$\frac{1}{2}\frac{{g}^{2}ta{n}^{2}��}{{q}^{2}}$ Ecos��
�����ܼ�СΪUABq=$\frac{1}{2}\frac{{g}^{2}ta{n}^{2}��}{q}cos��$
�𣺣�1��С�������ɣ��糡ǿ��Ϊ$\frac{mgtan��}{q}$
��2��AB����ĵ��Ʋ�UABΪ$\frac{1}{2}\frac{{g}^{2}ta{n}^{2}��}{q}cos��$
С������ܵı仯Ϊ$\frac{1}{2}\frac{{g}^{2}ta{n}^{2}��}{q}cos��$��
���� ����ʵ���Ͽ���������ƽ�⣬������������ֻҪ��ȷ��������������Ȼ�����ƽ�ⷽ����⼴�ɣ�����U=Ed����ĸ����

 ��ͼ��P��QΪ�������ֱ�Ϊ+q��-q�������������ֵ�ɣ��������L��OΪPQ���ߵ��е㣬M��NΪ�д����Ϲ���O��ԳƵ������㣬������
��ͼ��P��QΪ�������ֱ�Ϊ+q��-q�������������ֵ�ɣ��������L��OΪPQ���ߵ��е㣬M��NΪ�д����Ϲ���O��ԳƵ������㣬������| A�� | M��O��N����ij�ǿ����� | |
| B�� | M��N ����ij�ǿ��С��ȣ�������ͬ | |
| C�� | O��ij�ǿΪ�� | |
| D�� | �������ӽ��ܵ糡��������N�˶���M���ܱ��ֲ��� |
 ��ͼ��ʾ����һ���Ž���ˮƽ���ϹҼ����ڣ�����A��E�ڳ���ȣ�����A���������������������Ҳ�����������������ȶ�������
��ͼ��ʾ����һ���Ž���ˮƽ���ϹҼ����ڣ�����A��E�ڳ���ȣ�����A���������������������Ҳ�����������������ȶ�������| A�� | ���������������С��ͬ | |
| B�� | ��������ֻ��E�ڰڶ����ڸ�A����ͬ | |
| C�� | ���������������С����ͬ��E�������� | |
| D�� | �������������ڴ�С��ͬ��D��������� |

| A�� | ��1sĩ�ٶȸı䷽�� | B�� | ��2sĩλ�Ƹı䷽�� | ||
| C�� | ��4sĩλ����� | D�� | ��2sĩλ����� |
 һλ�����˶�Ա��ˮƽ������ת����Ϊm=4kg����������������Բ���˶�������T=1s��ת���뾶Ϊr=2.0m����
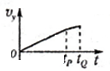
һλ�����˶�Ա��ˮƽ������ת����Ϊm=4kg����������������Բ���˶�������T=1s��ת���뾶Ϊr=2.0m���� ��ͼ��ʾ��ˮƽ�׳������壬�ִ�б���϶�P�������ٶȷ���ǡ����б�淽��Ȼ�����б����Ħ�����£����׳���Ϊԭ�㣬ˮƽ����Ϊx������ֱ����Ϊy������ֱ������ϵ�����й���������x��y�����˶����ٶ�-ʱ��ͼ������ȷ���ǣ�������
��ͼ��ʾ��ˮƽ�׳������壬�ִ�б���϶�P�������ٶȷ���ǡ����б�淽��Ȼ�����б����Ħ�����£����׳���Ϊԭ�㣬ˮƽ����Ϊx������ֱ����Ϊy������ֱ������ϵ�����й���������x��y�����˶����ٶ�-ʱ��ͼ������ȷ���ǣ�������


 ��ͼ��ʾ������Ϊm=0.3kg��С������Ϊq=-$\sqrt{3}$��10-3C���þ�Եϸ��������ˮƽ������ǿ�糡�У�С��ֹʱ��ϸ������ֱ����ɦ�=30��ǣ���С��������ǿ�糡�ij�ǿ��С������g=10m/s2��
��ͼ��ʾ������Ϊm=0.3kg��С������Ϊq=-$\sqrt{3}$��10-3C���þ�Եϸ��������ˮƽ������ǿ�糡�У�С��ֹʱ��ϸ������ֱ����ɦ�=30��ǣ���С��������ǿ�糡�ij�ǿ��С������g=10m/s2��