Question

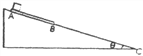
【题目】如图所示，在倾角的固定斜面上放置一质量kg、长度m的薄平板. 平板的上表面光滑，其下端与斜面底端的距离为16m. 在平板的上端处放一质量kg的滑块，开始时使平板和滑块都静止，之后将它们无初速释放. 设平板与斜面间、滑块与斜面间的动摩擦因数均为0.5，求：

(1)滑块从释放到刚离开平板所用时间

(2)滑块离开平板后，滑块与平板下端到达斜面底端的时间差. (，

g=10m/s2)

Answer 1

【答案】（1）1s （2）2s

【解析】试题分析：（1）对薄板，由于Mgsin37°＜μ（M+m）gcos37°，故滑块在薄板上滑动时，薄板静止不动，

对滑块：在薄板上滑行时加速度为：a1=gsin37°=6m/s2

离开板所需时间为L=at′2，

（2）到达B点时速度为：

滑块由B至C时的加速度为：a2=gsin37°-μgcos37°=2m/s2

设滑块由B至C所用时间为t，则有：LBC＝vt+a2t2

代入数据可解得：t=2s

对薄板，滑块滑离后才开始运动，加速度为：a3=gsin37°-μgcos37°=2m/s2

滑至C端所用时间为t'，则LBC＝a3t′2，代入数据可解得：t'=4s

滑块与平板下端B到达斜面底端C的时间差为：△t=t'-t=2s