Question

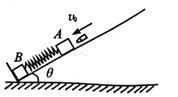
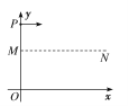
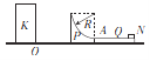
【题目】如图所示，光滑四分之一圆弧轨道P与木板Q在连接点A处通过一大小不计的感应开关连接(当滑块向右滑过A时，P、Q自动分离)。初始所有的物体均静止在光滑的水平地面上，滑块N从木板Q的右侧边缘处以v0=10m/s的初速度水平向左运动，到达A处时速度减小为v1=6m/s，接着滑上圆弧轨道P且恰好能到达P的最高点。滑块到达P的最高点时(物块未离开P)P在O点与物块K发生弹性碰撞，最后滑块停在木板上。滑块与木板之间的动摩擦因数μ=0.1，圆弧轨道的质量为3kg，木板与滑块的质量均为1kg，物块K的质量为5kg，重力加速度大小g=10m/s2，N可视为质点。求：

（1）木板的长度L；

（2）圆弧轨道的半径R；

（3）滑块与木板相对静止时，木板左端离O点的距离。

Answer 1

【答案】（1）30m；（2）1m；（3）1.425m

【解析】

(1)滑块、木板、圆弧轨道、物块的质量分别用m、MQ、MP、MK表示，滑块在木板Q上滑动的过程中，把P、Q和滑块作为一个系统，设滑块离开木板时，木板的速度为

根据动量守恒定律有

解得

滑块在木板Q上滑动的过程中，把P、Q和滑块作为一个系统，系统减少的动能全部转化为系统产生的热量，设木板的长度为L，根据功能关系有

解得

L=30m

(2)从滑块滑上圆弧轨道到圆弧轨道最高点的过程中，滑块和P、Q组成的系统水平方向动量守恒且机械能守恒，设滑块到达最高点时系统的速度为，根据动量守恒定律有

根据系统机械能守恒有

解得

R=1m

(3) P与K发生弹性碰撞，碰后滑块和P、Q瞬间共速，速度设为，K的速度为。根据弹性碰撞的特点，有

解得

以滑块在最高点为初状态，滑块滑回A为末状态，设滑回A处时滑块的速度大小为、P、Q的速度大小为，滑块和P、Q的位移大小分别为x1和x2，根据动量守恒定律和反冲，有

解得

滑块滑回A时P、Q分离，将滑块和木板看作一个系统，相对静止时的速度设为，滑块滑回A到相对静止时木板的位移为，滑块与木板相对静止时木板离O点的距离为x，根据动量守恒定律，有

根据动能定理，有

根据位置关系，可知

解得

x=1. 425m