��Ŀ����
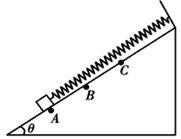
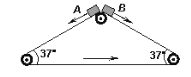
����Ŀ�������δ��ʹ��� 1m/s ���ٶ���ʱ������ת�������ߵĴ��ʹ������� 2m ����ˮƽ����ļнǾ�Ϊ 37������������С��� A��B �Ӵ��ʹ����˶��� 1m/s �ij��ٶ��ش��ʹ��»�������봫�ʹ���Ķ�Ħ���������� 0.5����g ȡ 10m/s2 ��sin37��=0.6��cos37��=0.8������˵����ȷ����( )
A. ��� A �ȵ��ﴫ�ʹ���
B. ��� A��B ͬʱ���ﴫ�ʹ���
C. ��� A��B ���ﴫ�ʹ���ʱ�ٶȴ�С�����
D. ��� A��B �ڴ��ʹ��ϵĻ��۳���֮��Ϊ 1:3
���𰸡�BD
��������
����A������б�����µķ�����Ħ�����Ĺ�ϵ���ж�A������˶����ɣ�B���ܵ�Ħ������б�����ϣ��������ȱ���ֱ���˶��������˶�ѧ��ʽ��˵�ʱ����ٶȣ�����˶�ѧ��ʽ������⻮�۳���֮�ȣ�
AB. ��A����Ϊmgsin37>��mgcos37����A��������Ħ������б�����ϣ��������ȼ���ֱ���˶���B����Ħ������б�����ϣ��������ȼ���ֱ���˶����������ȼ���ֱ���˶��ļ��ٶ���ȣ�λ����ȣ����˶���ʱ����ȡ���A����B��ȷ��
C.�����ٶ�ʱ���ϵv=at����� A��B ���ﴫ�ʹ���ʱ�ٶȴ�С��ȣ���C����
D. ��A�����۵ij��ȵ���A��λ�Ƽ�Ϊ���ʹ���λ�ƣ�
��AΪ�о�������ţ�ٵڶ����ɵã�mgsin37��-��mgcos37��=ma��a=2m/s2
���˶�ѧ��ʽ���˶�ʱ��ֱ�Ϊ��x=![]() at2��t=1s.
at2��t=1s.
����Ƥ���˶���λ��Ϊx=vt=1m.
����A��Ƥ���Ļ���Ϊ����x1=2m1m=1m
��B�����۵ij��ȵ���B��λ�Ƽ��ϴ��ʹ���λ�ƣ���x2=2m+1m=3m�����Ի���֮��Ϊ1:3����D��ȷ��
��ѡ��BD