题目内容
14.在“探究弹性势能的表达式”的实验中,为了计算弹簧弹力所做的功,把拉伸弹簧的过程分为很多小段,拉力为每小段可以认为是恒力,用各小段做的功的代数和代表弹力在整个过程所做的功,物理学中把这种研究方法叫做“微元法”.下面实例中应用到这一思想方法的是( )| A. | 根据加速度的定义a=$\frac{△v}{△t}$,当△t非常小,$\frac{△v}{△t}$就可以表示物体在t时刻的瞬时加速度 | |
| B. | 在探究加速度、力和质量三者之间关系时,先保持质量不变,研究加速度与力的关系,再保持力不变,研究加速度与质量的关系 | |
| C. | 在推导匀变速直线运动的位移公式时,把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,然后把各小段的位移相加 | |
| D. | 在不需要考虑物体本身的大小和形状时,用点来代替物体,即质点 |
分析 在物理学的重大发现中科学家们创造出了许多方法,如理想实验法,微元法,控制变量法,极限思想法、类比法和科学假说法等等.
解答 解:A、根据速度定义式$v=\frac{△x}{△t}$,当△t非常非常小时,$\frac{△x}{△t}$就可以表示物体在t时刻的瞬时速度,该定义应用了极限思想方法,故A错误.
B、研究多个变量时,应控制一些不变研究两个变量之间的关系,所以在探究加速度、力、质量三者之间的关系时,先保持质量不变研究加速度与力的关系,再保持力不变研究加速度与质量的关系,该实验运用了控制变量法,故B错误;
C、推导匀变速直线运动位移公式时,把整个运动过程划分成很多小段,每一段近似看成匀速直线运动,然后把各小段的位移相加,这里运用了微元法,故C正确.
D、在不需要考虑物体本身的大小和形状时,用质点来代替物体的方法是等效替代法,故D错误.
故选:C.
点评 本题考查对常用物理方法的掌握,我们要清楚一些物理概念的形成和定义方法和研究物理问题时所采用的研究方法和思想.

练习册系列答案
相关题目
8.某质点做曲线运动时( )
| A. | 在某时刻质点受到的合力可能为零 | |
| B. | 速度可能不变 | |
| C. | 在某一点的速度方向是该点曲线的切线方向 | |
| D. | 加速度一定发生改变 |
9.如图表示一交流电的电流随时间而变化的图象,此交流电流的有效值是( )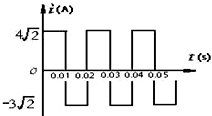

| A. | 4A | B. | 5A | C. | 4.5A | D. | 3.5A |
2.用铁锤把小铁钉钉入木板,设木板对钉子的阻力与钉进木板的深度成正比,已知铁锤第一次将钉子钉进d,如果铁锤第二次敲钉子时对钉子做的功与第一次相同,那么,第二次钉子进入木板的深度是( )
| A. | ($\sqrt{3}$-1)d | B. | ($\sqrt{2}$-1)d | C. | $\frac{\sqrt{51}}{2}$d | D. | $\frac{\sqrt{2}}{2}$d |
9.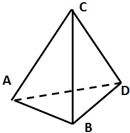 如图所示,正四面体所有棱长都相等长度为a,A、B、C、D是其四个顶点,现在B、D两点分别固定电量均为q的正负点电荷,静电力常量为k,下列说法正确的是( )
如图所示,正四面体所有棱长都相等长度为a,A、B、C、D是其四个顶点,现在B、D两点分别固定电量均为q的正负点电荷,静电力常量为k,下列说法正确的是( )
 如图所示,正四面体所有棱长都相等长度为a,A、B、C、D是其四个顶点,现在B、D两点分别固定电量均为q的正负点电荷,静电力常量为k,下列说法正确的是( )
如图所示,正四面体所有棱长都相等长度为a,A、B、C、D是其四个顶点,现在B、D两点分别固定电量均为q的正负点电荷,静电力常量为k,下列说法正确的是( )| A. | C点的场强大小为$\sqrt{3}$$\frac{kq}{{a}^{2}}$ | |
| B. | A、C两点的场强方向相同 | |
| C. | A、C两点电势相同 | |
| D. | 将一正电荷从A点沿直线移动到C点,电场力先做正功后做负功 |
19.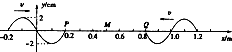 如图所示,两列简谐横波分别沿x轴正方向和负方向传播,两波源分别位于x=-0.2m和x=1.2m处,两列波的速度均为v=0.4m/s,两列波的振幅均为A=2cm,图示为t=0时刻两列波的图象(传播方向如图所示),此刻平衡位置处于x=0.2m和x=0.8m的P、Q两质点刚开始振动,质点M的平衡的位置处于x=0.5m处,关于各质点运动情况判断正确的是( )
如图所示,两列简谐横波分别沿x轴正方向和负方向传播,两波源分别位于x=-0.2m和x=1.2m处,两列波的速度均为v=0.4m/s,两列波的振幅均为A=2cm,图示为t=0时刻两列波的图象(传播方向如图所示),此刻平衡位置处于x=0.2m和x=0.8m的P、Q两质点刚开始振动,质点M的平衡的位置处于x=0.5m处,关于各质点运动情况判断正确的是( )
 如图所示,两列简谐横波分别沿x轴正方向和负方向传播,两波源分别位于x=-0.2m和x=1.2m处,两列波的速度均为v=0.4m/s,两列波的振幅均为A=2cm,图示为t=0时刻两列波的图象(传播方向如图所示),此刻平衡位置处于x=0.2m和x=0.8m的P、Q两质点刚开始振动,质点M的平衡的位置处于x=0.5m处,关于各质点运动情况判断正确的是( )
如图所示,两列简谐横波分别沿x轴正方向和负方向传播,两波源分别位于x=-0.2m和x=1.2m处,两列波的速度均为v=0.4m/s,两列波的振幅均为A=2cm,图示为t=0时刻两列波的图象(传播方向如图所示),此刻平衡位置处于x=0.2m和x=0.8m的P、Q两质点刚开始振动,质点M的平衡的位置处于x=0.5m处,关于各质点运动情况判断正确的是( )| A. | t=1s时刻,质点M的位移为-4m | B. | t=1s时刻,质点M的位移为4m | ||
| C. | t=0.75s时刻,质点P、Q都运动到M点 | D. | 质点P的起振方向沿y轴负方向 | ||
| E. | 质点Q的起振方向沿y轴负方向 |
6.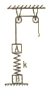 如图所示,物体A经一轻质弹簧与下方地面上物体B相连,弹簧的劲度系数为k,A、B质量均为m且都处于静止状态.一条不可伸长的轻绳绕过轻滑轮,一端连物体A,另一端连一轻挂钩.开始时各段绳都处于伸直状态,A上方的一段绳沿竖直方向,现在挂钩上挂一质量为m的物体C并从静止状态释放,已知它恰好能使B离开地面但不继续上升.若将物体C换成另一个质量为2m的物体D,仍从上述初始位置由静止状态释放,则这次物体B刚离地时,物体A的( )
如图所示,物体A经一轻质弹簧与下方地面上物体B相连,弹簧的劲度系数为k,A、B质量均为m且都处于静止状态.一条不可伸长的轻绳绕过轻滑轮,一端连物体A,另一端连一轻挂钩.开始时各段绳都处于伸直状态,A上方的一段绳沿竖直方向,现在挂钩上挂一质量为m的物体C并从静止状态释放,已知它恰好能使B离开地面但不继续上升.若将物体C换成另一个质量为2m的物体D,仍从上述初始位置由静止状态释放,则这次物体B刚离地时,物体A的( )
 如图所示,物体A经一轻质弹簧与下方地面上物体B相连,弹簧的劲度系数为k,A、B质量均为m且都处于静止状态.一条不可伸长的轻绳绕过轻滑轮,一端连物体A,另一端连一轻挂钩.开始时各段绳都处于伸直状态,A上方的一段绳沿竖直方向,现在挂钩上挂一质量为m的物体C并从静止状态释放,已知它恰好能使B离开地面但不继续上升.若将物体C换成另一个质量为2m的物体D,仍从上述初始位置由静止状态释放,则这次物体B刚离地时,物体A的( )
如图所示,物体A经一轻质弹簧与下方地面上物体B相连,弹簧的劲度系数为k,A、B质量均为m且都处于静止状态.一条不可伸长的轻绳绕过轻滑轮,一端连物体A,另一端连一轻挂钩.开始时各段绳都处于伸直状态,A上方的一段绳沿竖直方向,现在挂钩上挂一质量为m的物体C并从静止状态释放,已知它恰好能使B离开地面但不继续上升.若将物体C换成另一个质量为2m的物体D,仍从上述初始位置由静止状态释放,则这次物体B刚离地时,物体A的( )| A. | 加速度为零 | B. | 加速度为$\frac{1}{3}$g | C. | 动能为$\frac{{m}^{2}{g}^{2}}{3k}$ | D. | 动能为$\frac{2{m}^{2}{g}^{2}}{3k}$ |
 用密封性好、充满气体的塑料袋包裹易碎品,如图所示.充气袋四周被挤压时,假设袋内气体与外界无热交换,则袋内气体体积减小(填“增大”、“不 变”或“减小”),内能增大(填“增大”、“不变”或“减小,’),压强增大(填“增大”、“不变”或“减小,’),对外界做负功(填“做正功”、“做负 功”或“不做功”)
用密封性好、充满气体的塑料袋包裹易碎品,如图所示.充气袋四周被挤压时,假设袋内气体与外界无热交换,则袋内气体体积减小(填“增大”、“不 变”或“减小”),内能增大(填“增大”、“不变”或“减小,’),压强增大(填“增大”、“不变”或“减小,’),对外界做负功(填“做正功”、“做负 功”或“不做功”)