题目内容
1. 如图所示,半圆柱体重G,重心C到圆心O的距离为a=$\frac{4R}{3π}$,其中R为圆柱体半径.如果半圆柱体与水平面间的摩擦因数为μ,求该半圆柱体被拉动时所偏过的角度θ.
如图所示,半圆柱体重G,重心C到圆心O的距离为a=$\frac{4R}{3π}$,其中R为圆柱体半径.如果半圆柱体与水平面间的摩擦因数为μ,求该半圆柱体被拉动时所偏过的角度θ.
分析 对物体受力分析,考虑匀速滑动的情况,受力分析后根据力矩平衡条件列式求解即可;再根据平衡条件列式;最后联立求解即可.
解答  解:以半圆柱体与地面的切线为转轴,根据力矩平衡条件,拉力的力矩与重力的力矩平衡,故:
解:以半圆柱体与地面的切线为转轴,根据力矩平衡条件,拉力的力矩与重力的力矩平衡,故:
Gasinθ=F(R-Rsinθ) ①
根据平衡条件,有:
N=G
F=f
其中:
f=μN
解得:
F=μG ②
联立①②解得:
sinθ=$\frac{3μπ}{3μπ+4}$
故θ=arcsin$\frac{3μπ}{3μπ+4}$
答:该半圆柱体被拉动时所偏过的角度θ为arcsin$\frac{3μπ}{3μπ+4}$.
点评 本题是共点力平衡条件和力矩平衡条件的综合运用问题,关键是受力分析后根据平衡条件列式,要能够找出力矩,不难.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
11.产生光电效应时,关于逸出光电子的最大初动能Ek,下列说法正确的是 ( )
| A. | 对于同种金属,Ek与照射光的强度无关 | |
| B. | 对于同种金属,Ek与照射光的波长成反比 | |
| C. | 对于同种金属,Ek与光照射的时间成正比 | |
| D. | 对于同种金属,Ek与照射光的频率成线性关系 | |
| E. | 对于不同种金属,若照射光频率不变,Ek与金属的逸出功成线性关系 |
12.空间存在两个完全相同的间距为6m的振源m、n,空间另有一点p,已知pm⊥mn,且pm=8m,两振源形成的机械波在pmn所在的平面内传播.某时刻两振源m、n同时振动,其振动图象如图乙所示,在4s时p点刚开始振动.则下列说法正确的是( )

| A. | 波速为2m/s | |
| B. | 当两列波均传到p点时,p点的振动频率加倍 | |
| C. | 波长为2m | |
| D. | p点为振动加强点 | |
| E. | p点为振动减弱点 |
9.小明在研究点电荷周围的电场的实验时,在x轴上放一个点电荷Q(图中未画出),O、A、B为轴上三点,如图(甲)所示.测得放在A、B两点的检验电荷受到的电场力跟检验电荷所带电荷量的关系如图(乙)所示.以x轴的正方向为电场力的正方向,则正确的是( )


| A. | 点电荷Q一定为正电荷 | B. | 点电荷Q在AB之间 | ||
| C. | A点的电势比B点的电势高 | D. | A点的电场强度大小为2×103N/C |
16. 如图,用绝缘细线悬挂一个带正电的铜制圆环,悬挂于O点,摆长为L,当它摆过竖直线OC时便进入或离开一个匀强磁场,磁场方向垂直于圆环摆动的平面,A、D点分别是最大位移处,下列说法中正确的是( )
如图,用绝缘细线悬挂一个带正电的铜制圆环,悬挂于O点,摆长为L,当它摆过竖直线OC时便进入或离开一个匀强磁场,磁场方向垂直于圆环摆动的平面,A、D点分别是最大位移处,下列说法中正确的是( )
 如图,用绝缘细线悬挂一个带正电的铜制圆环,悬挂于O点,摆长为L,当它摆过竖直线OC时便进入或离开一个匀强磁场,磁场方向垂直于圆环摆动的平面,A、D点分别是最大位移处,下列说法中正确的是( )
如图,用绝缘细线悬挂一个带正电的铜制圆环,悬挂于O点,摆长为L,当它摆过竖直线OC时便进入或离开一个匀强磁场,磁场方向垂直于圆环摆动的平面,A、D点分别是最大位移处,下列说法中正确的是( )| A. | A点和D点处于同一水平面 | |
| B. | 圆环每次经过C点时的速度相同 | |
| C. | 圆环在摆动过程中机械能不守恒 | |
| D. | 圆环每次经过E点时,绳上的拉力不等 |
10.某多用电表欧姆挡“×1”的内部电路图如图1所示,小明同学将电阻箱R和电压表V并联后接在两表笔a、b上,欲用图示的电路测量多用电表内部的电阻r(远小于电压表V的内阻)和电池的电动势E.实验的主要步骤为:
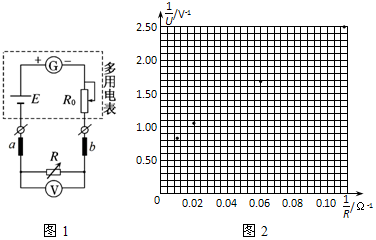
(1)表笔a为红表笔(填“红表笔”或“黑表笔”).将选择开关转至欧姆挡“×1”,将红黑表笔短接,调节R0,使指针指在右(填“左”或“右”)侧零刻度处.
(2)改变电阻箱R的阻值,分别读出6组电压表和电阻箱的示数U、R,将$\frac{1}{U}$、$\frac{1}{R}$的值算出并记录在表格中,请将第3、5组数据的对应点在图2坐标纸上补充标出,并作出$\frac{1}{U}$-$\frac{1}{R}$图线.
(3)根据图线得到电动势E=1.42V,内电阻r=2.41Ω.(结果均保留三位有效数字)

(1)表笔a为红表笔(填“红表笔”或“黑表笔”).将选择开关转至欧姆挡“×1”,将红黑表笔短接,调节R0,使指针指在右(填“左”或“右”)侧零刻度处.
(2)改变电阻箱R的阻值,分别读出6组电压表和电阻箱的示数U、R,将$\frac{1}{U}$、$\frac{1}{R}$的值算出并记录在表格中,请将第3、5组数据的对应点在图2坐标纸上补充标出,并作出$\frac{1}{U}$-$\frac{1}{R}$图线.
| 组数 | 1 | 2 | 3 | 4 | 5 | 6 |
| R | 100.0 | 50.0 | 25.0 | 16.7 | 12.5 | 9.1 |
| $\frac{1}{R}$ | 0.01 | 0.02 | 0.04 | 0.06 | 0.08 | 0.11 |
| U | 1.20 | 0.95 | 0.74 | 0.60 | 0.50 | 0.40 |
| $\frac{1}{U}$ | 0.83 | 1.05 | 1.35 | 1.68 | 2.00 | 2.50 |
 如图甲所示,在光滑绝缘的水平桌面上建立一xoy坐标系,平面处在周期性变化的电场和磁场中,电场和磁场的变化规律如图乙所示(规定沿+y方向为电场强度的正方向,竖直向下为磁感应强度的正方向).在t=0时刻,一质量为m=0.01kg、电荷量为q=0.1C的带电金属小球自坐标原点O处,以v0=2m/s的速度沿x轴正方向射出.已知E0=0.2N/C、B0=0.2π T.求:
如图甲所示,在光滑绝缘的水平桌面上建立一xoy坐标系,平面处在周期性变化的电场和磁场中,电场和磁场的变化规律如图乙所示(规定沿+y方向为电场强度的正方向,竖直向下为磁感应强度的正方向).在t=0时刻,一质量为m=0.01kg、电荷量为q=0.1C的带电金属小球自坐标原点O处,以v0=2m/s的速度沿x轴正方向射出.已知E0=0.2N/C、B0=0.2π T.求: 如图所示为一表面带有均匀负电荷的导体板MNO,其中MN与NO衔接于N点,MN水平且长为1m,NO长为0.6m,其中NO与MN的夹角为θ=37°,一带正电的绝缘滑块由M点以水平向左的初速度v0=4m/s滑上导体板,其中滑块与导体板间的库仑引力为滑块重力的0.2倍,两者间的动摩擦因数为μ=0.25,只考虑滑块运动轨迹所在处电荷对滑块垂直接触面的库仑引力,滑块在N处的能量损失不计.(sin 37°=0.6,cos 37°=0.8,g取10m/s2)
如图所示为一表面带有均匀负电荷的导体板MNO,其中MN与NO衔接于N点,MN水平且长为1m,NO长为0.6m,其中NO与MN的夹角为θ=37°,一带正电的绝缘滑块由M点以水平向左的初速度v0=4m/s滑上导体板,其中滑块与导体板间的库仑引力为滑块重力的0.2倍,两者间的动摩擦因数为μ=0.25,只考虑滑块运动轨迹所在处电荷对滑块垂直接触面的库仑引力,滑块在N处的能量损失不计.(sin 37°=0.6,cos 37°=0.8,g取10m/s2)