题目内容
6. 如图甲所示,在光滑绝缘的水平桌面上建立一xoy坐标系,平面处在周期性变化的电场和磁场中,电场和磁场的变化规律如图乙所示(规定沿+y方向为电场强度的正方向,竖直向下为磁感应强度的正方向).在t=0时刻,一质量为m=0.01kg、电荷量为q=0.1C的带电金属小球自坐标原点O处,以v0=2m/s的速度沿x轴正方向射出.已知E0=0.2N/C、B0=0.2π T.求:
如图甲所示,在光滑绝缘的水平桌面上建立一xoy坐标系,平面处在周期性变化的电场和磁场中,电场和磁场的变化规律如图乙所示(规定沿+y方向为电场强度的正方向,竖直向下为磁感应强度的正方向).在t=0时刻,一质量为m=0.01kg、电荷量为q=0.1C的带电金属小球自坐标原点O处,以v0=2m/s的速度沿x轴正方向射出.已知E0=0.2N/C、B0=0.2π T.求:(1)t=1s末金属小球速度的大小和方向;
(2)1s~2s内,金属小球在磁场中做圆周运动的半径和周期;
(3)试求出第3秒末小球所在位置的坐标.
分析 (1)金属球在0-1s内做类平抛运动,分别求出x、y轴方向的分速度,然后求出小球的速度.
(2)金属球做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律可以求出半径与周期.
(3)金属球在第1与第3秒内都沿x轴做匀速直线运动,沿y轴做匀加速直线运动,在第2s内金属球做匀速圆周运动,应用匀速与匀变速直线运动的运动规律可以求出小球的坐标.
解答 解:(1)在0~1s内,金属小球做类平抛运动,
x轴方向:vx=v0=2m/s,
y方向:vy=at1=$\frac{q{E}_{0}}{m}$t1=$\frac{0.1×0.2}{0.01}$×1=2m/s,
1s末粒子的速度:v1=$\sqrt{{v}_{x}^{2}+{v}_{y}^{2}}$=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$m/s,
设v1与x轴正方向的夹角为α,则:tanα=$\frac{{v}_{y}}{{v}_{x}}$=$\frac{2}{2}$=1,则α=45°;
(2)在1s~2s内,粒子在磁场中做圆周运动,洛伦兹力提供向心力,
由牛顿第二定律得:qv1B0=m$\frac{{v}_{1}^{2}}{r}$,代入数据解得:r=$\frac{\sqrt{2}}{π}$m,
粒子做圆周运动的周期:T=$\frac{2πr}{{v}_{1}}$,解得:T=1s;
(3)由(2)可知小球在第2秒的位置和第1秒末的位置相同,
金属球在第三秒内沿x轴做匀速直线运动,沿y轴做匀加速直线运动,
设第3秒末小球所处位置坐标为(x,y),t2=2s,
在x轴方向:x=v0t2,
在y轴方向:y=$\frac{1}{2}$$\frac{q{E}_{0}}{m}$t22,
代入数据解得:x=4m,y=4m,金属球的坐标为:(4m,4m);
答:(1)t=1s末金属小球速度的大小为$\sqrt{2}$m/s,方向:与x轴正方向夹45°角;
(2)1s~2s内,金属小球在磁场中做圆周运动的半径为$\frac{\sqrt{2}}{π}$m,周期为1s;
(3)第3秒末小球所在位置的坐标为(4m,4m).
点评 金属球在电场中受到电场力作用,在磁场中受到洛伦兹力作用,根据图示图象分析清楚金属球的运动过程,应用匀速运动规律与匀变速运动规律即可正确解题.

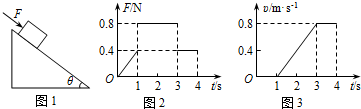
| A. | 物块的质量为1kg | |
| B. | 物块与斜面间的动摩擦因数为0.7 | |
| C. | 0~3s时间内力F做功的平均功率为0.32W | |
| D. | 0~3s时间内物体克服摩擦力做的功为5.12J |
 在珠海航展中,中国展出了国产运-20和歼-31等最先进飞机.假设航展中有两飞机甲、乙在平直跑道上同向行驶,0-t2时间内的v-t图象如图所示,下列说法正确的是( )
在珠海航展中,中国展出了国产运-20和歼-31等最先进飞机.假设航展中有两飞机甲、乙在平直跑道上同向行驶,0-t2时间内的v-t图象如图所示,下列说法正确的是( )| A. | 飞机乙在0-t2内的平均速度等于$\frac{v_2}{2}$ | |
| B. | 飞机甲在0-t2内的平均速度的比乙大 | |
| C. | 两飞机在t1时刻一定相遇 | |
| D. | 两飞机在0-t2内不可能相遇 |
 如图所示,真空中有一个半径为R,质量均匀分布的玻璃球,由a、b两种单色光组成的复合光束射入该玻璃球,当入射角θ等于60°时,其折射光束和出射光束如图所示.已知a光束第一次射出此玻璃球后的出射光束相对复合光束的偏转角也为60°,c为真空中的光速,则下列说法正确的是( )
如图所示,真空中有一个半径为R,质量均匀分布的玻璃球,由a、b两种单色光组成的复合光束射入该玻璃球,当入射角θ等于60°时,其折射光束和出射光束如图所示.已知a光束第一次射出此玻璃球后的出射光束相对复合光束的偏转角也为60°,c为真空中的光速,则下列说法正确的是( )| A. | a光在玻璃中穿越的时间为t=$\frac{3R}{c}$ | |
| B. | 用同一装置分别进行双缝干涉实验时,b光的亮条纹间距比a光大些 | |
| C. | a、b光从真空进入玻璃球,其频率将变小 | |
| D. | 适当增大入射角θ,a、b光束都可能发生全反射 |
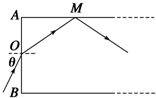
 一个闭合的正方形金属线框放入如图所示的匀强磁场中,图中虚线表示磁场的边界,在外力作用下线框从磁场中以速度v匀速穿出.关于线框从磁场边界穿出过程,下列说法中正确的是( )
一个闭合的正方形金属线框放入如图所示的匀强磁场中,图中虚线表示磁场的边界,在外力作用下线框从磁场中以速度v匀速穿出.关于线框从磁场边界穿出过程,下列说法中正确的是( )| A. | 线框的运动速度越大,通过导线横截面的电荷量越多 | |
| B. | 磁感应强度越大,拉力的功率越大 | |
| C. | 线框的电阻越大,导线中产生的热量越多 | |
| D. | 线框的边长与拉力做功的多少无关 |
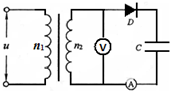 如图所示,理想变压器原、副线圈匝数之比为n1:n2=22:1,原线圈接220V的正弦交变电压,副线圈连接理想交流电压表V、交流电流表A、理想二极管D和电容器C.则下述结论错误的是( )
如图所示,理想变压器原、副线圈匝数之比为n1:n2=22:1,原线圈接220V的正弦交变电压,副线圈连接理想交流电压表V、交流电流表A、理想二极管D和电容器C.则下述结论错误的是( )| A. | 电压表的示数为10 V | |
| B. | 稳定后电流表的读数为零 | |
| C. | 电容器不断地充电和放电,电量不断变化 | |
| D. | 稳定后电容器两极板间电势差始终为10$\sqrt{2}$ V |
 光纤通信之所以能进行远距离通信,主要是利用了光的全反射原理.
光纤通信之所以能进行远距离通信,主要是利用了光的全反射原理. 如图所示,半圆柱体重G,重心C到圆心O的距离为a=$\frac{4R}{3π}$,其中R为圆柱体半径.如果半圆柱体与水平面间的摩擦因数为μ,求该半圆柱体被拉动时所偏过的角度θ.
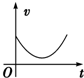
如图所示,半圆柱体重G,重心C到圆心O的距离为a=$\frac{4R}{3π}$,其中R为圆柱体半径.如果半圆柱体与水平面间的摩擦因数为μ,求该半圆柱体被拉动时所偏过的角度θ. 如图所示,一带电粒子仅在电场力的作用下,沿一直的电场线从A点运动到B点,则关于此带电粒子运动的v-t图象,可能正确的是( )
如图所示,一带电粒子仅在电场力的作用下,沿一直的电场线从A点运动到B点,则关于此带电粒子运动的v-t图象,可能正确的是( )