题目内容
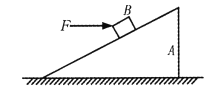
【题目】如图所示,一光滑的斜面与一光滑平台平滑连接,平台的右端恰好在四分之一圆弧的圆心,圆弧的半径为R,质量为m的物体B,放在平台的右端,质量为M的A物体从某一高度下滑,A下滑到平台右端和B物体相碰,碰后B物体做平抛运动,落到圆弧上,则

(1)若落点与圆心连线与水平方向夹角为![]() ,求B物体碰后瞬间的速度。
,求B物体碰后瞬间的速度。
(2)若该落点比落在其他地方的动能都小,求B物体碰后瞬间的速度。
(3)试求满足第(2)问条件时,A物体开时下滑时高度的可能值。
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】:(1)设B物体落地点与圆心的连线和水平面夹角为θ,B物体与A碰后的速度为v。落到圆弧轨道的时间为t,根据平抛运动知识有:
Rcosθ=vt ![]()
解得:![]()
(2)设B物体落到圆弧上的动能为Ek,根据动能定理有:
![]()
联立解得:![]()
当![]() 时,Ek最小,解得B物体平抛初速度v为:
时,Ek最小,解得B物体平抛初速度v为:![]()
(3)设A与B碰前速度为v0,A与B碰撞后的速度为v1,由动量守恒有:
Mv0=Mv1+mv
A与B碰后,应有:![]()
A与B碰撞可能有动能损失,则有:![]()
联立解得:![]()
在A下滑的过程中,根据动能定理,有:![]()
联立解得:![]()

练习册系列答案
相关题目