题目内容
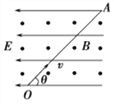
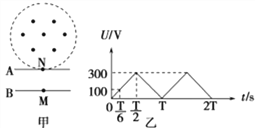
【题目】在图甲中，加速电场A、B板水平放置，半径R＝0.2 m的圆形偏转磁场与加速电场的A板相切于N点，有一群比荷为
＝5×105 C/kg的带电粒子从电场中的M点处由静止释放，经过电场加速后，从N点垂直于A板进入圆形偏转磁场，加速电场的电压U随时间t的变化如图乙所示，每个带电粒子通过加速电场的时间极短，可认为加速电压不变. 
时刻进入电场的粒子恰好水平向左离开磁场，(不计粒子的重力)求：
(1)粒子的电性；
(2)磁感应强度B的大小；
(3)何时释放的粒子在磁场中运动的时间最短？最短时间t是多少(π取3)．
【答案】(1) 负电 (2) B＝0.1 T (3) t＝2×10－5 s
【解析】（1）由题意可知，粒子水平向左离开磁场，则粒子所受洛伦兹力向左，根据左手定则得，粒子带负电；
（2）由图示图象可知，当
时，U=100V，
根据动能定理得： 
，
粒子做圆周运动洛伦兹力提供向心力，
由牛顿第二定律得： 
粒子恰好水平向左离开磁场，粒子轨道半径：r1=R
解得：B=0.1T；
（3）速度越大，粒子在磁场中运动的半径越大，时间越短，当t＝kT+
（k=0、1、2、3…）时进入电场的粒子在磁场中运动的时间最短，
根据动能定理得： 
根据牛顿第二定律得： 
由几何关系得： 
根据周期公式得： 
，粒子在磁场中的运动时间： 
解得：t=2×10-5s；
练习册系列答案
相关题目
