题目内容
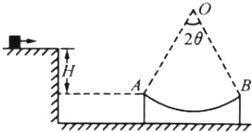 如图所示,光滑水平桌面上有一质量为m的物块,桌面右下方有半径为R的光滑圆弧形轨道,圆弧所对应的圆心角为2θ,轨道左右两端点A、B等高,左端A与桌面的右端的高度差为H.已知物块在一向右的水平拉力作用下沿桌面由静止滑动,撤去拉力后物块离开桌面,落到轨道左端时其速度方向与轨道相切,随后沿轨道滑动,若轨道始终与地面保持相对静止,求:(重力加速度为g)
如图所示,光滑水平桌面上有一质量为m的物块,桌面右下方有半径为R的光滑圆弧形轨道,圆弧所对应的圆心角为2θ,轨道左右两端点A、B等高,左端A与桌面的右端的高度差为H.已知物块在一向右的水平拉力作用下沿桌面由静止滑动,撤去拉力后物块离开桌面,落到轨道左端时其速度方向与轨道相切,随后沿轨道滑动,若轨道始终与地面保持相对静止,求:(重力加速度为g)(1)拉力对物块做的功;
(2)物块滑至轨道的最低点时受到支持力大小.
分析:(1)物体离开平台后做平抛运动,由竖直方向上的运动规律可求得竖直分速度;再由运动的合成与分解可求得水平分速度;再对平台上的运动由动能定理可求得拉力所做的功;
(2)由运动的合成与分解可求得A点的合速度;现由机械能守恒可求得物体到达底部时的速度;由向心力公式可求得支持力大小.
(2)由运动的合成与分解可求得A点的合速度;现由机械能守恒可求得物体到达底部时的速度;由向心力公式可求得支持力大小.
解答:解:(1)物块在桌面上滑动过程中,由动能定理有:
WF=
mv20
离开桌面时竖直方向上有:v2y=2gH,
又v0=
,
联立解得:WF=
.
(2)由图可得:v1=
,
从轨道左端到底端物体机械能守恒,则有:
mv21+mgR(1-cosθ)=
mv22
在最底端时由牛顿第二定律得:
F-mg=m
,
联立解得:F=mg(3-2cosθ)+
答:(1)拉力对物体所做的功为
;
(2)物块滑至轨道的最低点的支持力大小为mg(3-2cosθ)+
.
WF=
| 1 |
| 2 |
离开桌面时竖直方向上有:v2y=2gH,
又v0=
| vy |
| tanθ |
联立解得:WF=
| mgH |
| tan2θ |
(2)由图可得:v1=
| vy |
| sinθ |
从轨道左端到底端物体机械能守恒,则有:
| 1 |
| 2 |
| 1 |
| 2 |
在最底端时由牛顿第二定律得:
F-mg=m
| ||
| R |
联立解得:F=mg(3-2cosθ)+
| 2mgH |
| Rsin2θ |
答:(1)拉力对物体所做的功为
| mgH |
| tan2θ |
(2)物块滑至轨道的最低点的支持力大小为mg(3-2cosθ)+
| 2mgH |
| Rsin2θ |
点评:本题考查动能定理、机械能守恒以及向心力公式的应用,同时在平抛运动中要注意运动的合成与分解的应用.

练习册系列答案
相关题目
 如图所示,光滑水平桌面上,有甲、乙两个用细线相连的物体在水平拉力F1和F2的作用下运动,已知F1<F2,则以下说法中错误的有( )
如图所示,光滑水平桌面上,有甲、乙两个用细线相连的物体在水平拉力F1和F2的作用下运动,已知F1<F2,则以下说法中错误的有( )| A、若撤去F1,则甲的加速度一定变大 | B、若撤去F1,则细线上的拉力一定变小 | C、若撤去F2,则细线上的拉力一定变小 | D、若撤去F2,则乙的加速度一定变大 |
 如图所示,光滑水平桌面上,有甲、乙两个用细线相连的物体在水平拉力F1和F2的作用下运动,已知F1<F2,则以下说法中正确的有( )
如图所示,光滑水平桌面上,有甲、乙两个用细线相连的物体在水平拉力F1和F2的作用下运动,已知F1<F2,则以下说法中正确的有( ) (2013?常州模拟)如图所示,光滑水平桌面上,一小球以速度v向右匀速运动,当它经过靠近桌边的竖直木板ad边前方时,木板开始作自由落体运动.若木板开始运动时,cd边与桌面相 齐,则小球在木板上的投影轨迹是( )
(2013?常州模拟)如图所示,光滑水平桌面上,一小球以速度v向右匀速运动,当它经过靠近桌边的竖直木板ad边前方时,木板开始作自由落体运动.若木板开始运动时,cd边与桌面相 齐,则小球在木板上的投影轨迹是( ) (2012?广东二模)如图所示,光滑水平桌面上,有甲、乙两个用轻质细线相连的物体在水平拉力F1和F2的作用下运动,已知F1<F2,则以下说法中正确的有( )
(2012?广东二模)如图所示,光滑水平桌面上,有甲、乙两个用轻质细线相连的物体在水平拉力F1和F2的作用下运动,已知F1<F2,则以下说法中正确的有( ) 如图所示放在光滑水平桌面上的A、B木块中部夹一被压缩的弹簧,当弹簧被放开时,它们各自在桌面上滑行一段距离后,飞离桌面落在地上.A的落地点与桌边水平距离0.5米,B的落地点距离桌边1米,那么( )
如图所示放在光滑水平桌面上的A、B木块中部夹一被压缩的弹簧,当弹簧被放开时,它们各自在桌面上滑行一段距离后,飞离桌面落在地上.A的落地点与桌边水平距离0.5米,B的落地点距离桌边1米,那么( )