题目内容
5. 如图在一个分布范围足够大的水平向右的匀强电场中,用长为L的绝缘轻质细丝线把一个带电小球悬挂在O点,小球的质量为m,带电量为q,现把小球用绝缘工具移动到B位置,使细丝线伸直且水平,无初速释放小球,小球向左能够到达的最远位置为D,小球速度最大位置为A,小球在D、A两位置时,细丝线与竖直方向的夹角分别为α、θ,且θ=30°.试求:
如图在一个分布范围足够大的水平向右的匀强电场中,用长为L的绝缘轻质细丝线把一个带电小球悬挂在O点,小球的质量为m,带电量为q,现把小球用绝缘工具移动到B位置,使细丝线伸直且水平,无初速释放小球,小球向左能够到达的最远位置为D,小球速度最大位置为A,小球在D、A两位置时,细丝线与竖直方向的夹角分别为α、θ,且θ=30°.试求:(1)匀强电场的场强E
(2)图中α角的大小.
分析 (1)小球速度最大位置为A,细丝线与竖直方向夹角为θ=30°,此时必有重力与电场力的合力与细线在一条线上,据此求解E.
(2)小球从B到D的过程,由动能定理列式求解图中α角的大小
解答 解:(1)小球速度最大位置为A,细丝线与竖直方向夹角为θ=30°,此时必有重力与电场力的合力与细线在一条线上,故有: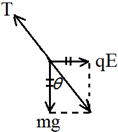
qE=mgtanθ
整理得:E=$\frac{mgtan30°}{q}=\frac{\sqrt{3}mg}{3q}$;
(2)小球从B到D的过程,由动能定理得:
W总=mgLcosα-qEL(1+sinα)=0
带入数据得:α=30°(另一解舍去)
答:(1)匀强电场的场强为 (2)小球向左能够到达的最远位置为D,小球在D位置时,细丝线与竖直方向的夹角α=30°
点评 本题是力学知识与电场知识的综合,关键是分析清楚小球的受力情况和做功情况,运用动能定理和牛顿第二定律求解.

练习册系列答案
相关题目
 图为一列横波在某一时刻的波形图,若此时质点Q的速度方向沿y轴负方向,则
图为一列横波在某一时刻的波形图,若此时质点Q的速度方向沿y轴负方向,则 要测量一个电源的电动势E(小于3V)和内阻r(约为1Ω),现有下列器材:电压表V(3V和15V两个量程)、电阻箱(0~999.9Ω)、定值电阻R0=2Ω、开关和导线.某实验小组根据所给器材设计了如图甲所示的实验电路.
要测量一个电源的电动势E(小于3V)和内阻r(约为1Ω),现有下列器材:电压表V(3V和15V两个量程)、电阻箱(0~999.9Ω)、定值电阻R0=2Ω、开关和导线.某实验小组根据所给器材设计了如图甲所示的实验电路.




