题目内容
【题目】如图所示，左边圆柱形容器的横截面积为S，上端是一个可以在容器内无摩擦滑动的质量为m的活塞；右边圆柱形容器上端封闭高为H，横截面积为
。两容器由装有阀门的极细管道相连，容器、活塞和细管都是绝热的。开始时阀门关闭，左边容器中装有理想气体，平衡时活塞到容器底的距离为H，右边容器内为真空。现将阀门打开，活塞缓慢下降，直至系统达到新的平衡，此时气体的热力学温度增加到原来热力学温度的1.3倍。已知外界大气压强为p，求：
(i)系统达到新的平衡时活塞到容器底的距离r；
(ii)此过程中容器内的气体内能的增加量U。
【答案】(i)
(ii)
【解析】
(i)设阀门打开前气体的热力学温度为T，由盖－吕萨克定律有：
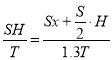
解得：
(ii)设容器内的气体压强为p，取活塞为研究对象，有：
外界对气体所做的功为：
由系统绝热有：
Q=0
由热力学第一定律有：ΔU=W，解得：
练习册系列答案
中考解读考点精练系列答案
相关题目
