��Ŀ����
3����ͼ��ʾ������ԴS���Բ��ϲ�������Ϊm�������Ϊ+q�����ӣ��������ƣ������Ӵ�O1��Ʈ��һ��ˮƽ����ļ��ٵ糡�����ٲ��ƣ����پ���С��O2�������������ǿ�糡����ǿ�ų����糡ǿ�ȴ�СΪE���Ÿ�Ӧǿ�ȴ�СΪB1��������ͼ������PQ��MN֮�������ˮƽ���ҵ���ǿ�ų����ų���Χ�㹻�Ÿ�Ӧǿ�ȴ�СΪB2��һ���۳�ֱ�ǵ�Ӳ������Ƭabc�������磬���Ⱥͺ�ȶ���С�ɺ��ԣ�ab�ߡ�bc��Ϊ����Ƭ��ac��Ϊȱ�ڣ�������PQ��MN֮�䣬����ͼ��ͼ��a��c����ֱ�λ��PQ��MN�ϣ�ab=bc=L����=45�㣮��������ͼ������O2O3���ӳ��߽���PQ��MN֮�������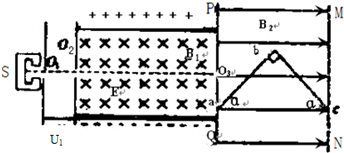
��1������ٵ�ѹU1��
��2������������Ӳ������Ƭ�������ٶȴ�С���䣬������ѭ��ķ��䶨�ɣ���ô����������Ƭ��һ�������ڶ�������ǰ��ʲô�˶���
��3��������PQ��MN֮����������˶�����ʱ��t����·��s��
���� ��1�����Ӿ������ϳ�ʱ���糡�����£������������ϣ������ٶȴ�ֱ���ʺ���Ϊ�㣬����ƽ��������ʽ����ٶȣ�
��2��������ų���һ����ײ���ٶ����ϣ����������ṩ������������ac�ߴ�ֱ��ƽ����������Բ���˶�������һȦ����ab���ڲ���ײ����ײ��ˮƽ�����˶�����bc�߶�����ײ������ac�ߴ�ֱ��ƽ�������ٴ�����Բ���˶����־���һȦ����b�������ײ��ˮƽ�����뿪�ų���
��3���ȷ������˶��켣���ٷ�����ֱ���˶�������Բ���˶����ۣ���������Բ���˶����ȼ���뾶�����ڣ��ٸ��ݹ켣���㣮
��� �⣺��1�����������������������˶���Eq=qv0B1��
��ã�v0=$\frac{E}{{B}_{1}}$��
�ɶ��ܶ����ã�qU1=$\frac{1}{2}$mv02-0��
��ã�U1=$\frac{m{E}^{2}}{2q{B}_{1}^{2}}$��
��2����������ab���Դ�СΪv0���ٶȴ�ֱ�ų������˶������������������ڴ�ֱ�ڴų���ƽ����������Բ���˶���ת��һ�ܺ�ﵽab���²���
��3����ţ�ٵڶ����ɵã�qv0B2=m$\frac{{v}_{0}^{2}}{R}$��
��ã�R=$\frac{mE}{q{B}_{1}{B}_{2}}$��
�����ڴų�����Բ���˶�������Ϊ��T=$\frac{2��m}{q{B}_{2}}$��
�����ڴų��й�����2�Σ���Բ���˶���ʱ��Ϊ��t1=2T=$\frac{4��m}{q{B}_{2}}$��
��Բ���˶���·��Ϊ��s1=2•2��R=$\frac{4��mE}{q{B}_{1}{B}_{2}}$��
��ˮƽ�������˶���·��Ϊ��s2=$\sqrt{2}$R��
������ʱ��Ϊ��t2=$\frac{s}{{v}_{0}}$=$\frac{\sqrt{2}{B}_{1}L}{E}$��
��������PQ��MN֮����������˶�����ʱ��Ϊ��t=t1+t2=$\frac{4��m}{q{B}_{2}}$+$\frac{\sqrt{2}{B}_{1}L}{E}$��
��·��Ϊ��s=s1+s2=$\frac{4��mE}{q{B}_{1}{B}_{2}}$+$\sqrt{2}$R��
�𣺣�1�����ٵ�ѹU1Ϊ$\frac{m{E}^{2}}{2q{B}_{1}^{2}}$��
��2��������Բ���˶���
��3��������PQ��MN֮����������˶�����ʱ��tΪ$\frac{4��m}{q{B}_{2}}$+$\frac{\sqrt{2}{B}_{1}L}{E}$����·��sΪ$\frac{4��mE}{q{B}_{1}{B}_{2}}$+$\sqrt{2}$R��
���� �����еĸ��ϳ������ٶ�ѡ��Ĺ��ܣ�����ų�������ݶ���ѧ������ȷ���˶��켣���ٽ��м��㣮

 ��ͼ��ʾ����������A���ȼ���������ͬʱ��ʹ������ˮƽ����������ֱ���˶����������ʵ���˶��Ĺ켣�ǣ�������
��ͼ��ʾ����������A���ȼ���������ͬʱ��ʹ������ˮƽ����������ֱ���˶����������ʵ���˶��Ĺ켣�ǣ�������| A�� | ����Q | B�� | ֱ��P | C�� | ����R | D�� | ��ȷ�� |
 ��ͼ1��ʾ��һ��������ڴֲڵ�ˮƽ�����ϣ���t=0ʱ�̣�������ˮƽ��F�������ɾ�ֹ��ʼ��ֱ���˶�����0��t0ʱ��������ļ��ٶ�a��ʱ��t�ı仯������ͼ2��ʾ����֪����������Ķ�Ħ������������ȣ�������
��ͼ1��ʾ��һ��������ڴֲڵ�ˮƽ�����ϣ���t=0ʱ�̣�������ˮƽ��F�������ɾ�ֹ��ʼ��ֱ���˶�����0��t0ʱ��������ļ��ٶ�a��ʱ��t�ı仯������ͼ2��ʾ����֪����������Ķ�Ħ������������ȣ�������| A�� | t0ʱ�̣���F����0 | |
| B�� | ��0��t0ʱ���ڣ���F��С�㶨 | |
| C�� | ��0��t0ʱ���ڣ�������ٶ���� | |
| D�� | ��t0ʱ�̣�������ٶ���� |
| A�� | $\frac{4P}{m{v}_{m}}$ | B�� | $\frac{3P}{m{v}_{m}}$ | C�� | $\frac{2P}{m{v}_{m}}$ | D�� | $\frac{P}{m{v}_{m}}$ |
| A�� | ������Ȼ�����������������ʹ������ʶ��ԭ�Ӿ��и��ӵĽṹ | |
| B�� | ¬ɪ�����ԭ�ӵĺ�ʽ�ṹģ�ͽ����Ļ����Ǧ����ӵ�ɢ��ʵ�� | |
| C�� | ԭ�Ӻ��ڵ�ijһ�������������Ӽ䶼�к������� | |
| D�� | �Ƚ���ܴ��ԭ�Ӻ˷ֽ�ɱȽ����С��ԭ�Ӻ�ʱҪ�ų����� |
 ��ͼ��ʾ���ھ�Ե�ֲ�ˮƽ���Ϸ����������㹻���ˮƽ���ҵ���ǿ�糡���������С��������һ�����ٶȴ�A�㿪ʼ��ˮƽ��������ֱ���˶�����L���ȵ���B�㣬�ٶȱ�Ϊ�㣬�˹����н�������ʧ�Ķ�����$\frac{3}{4}$ת��Ϊ�����ܣ�����������˶���ij��C��ͼ��δ�����ʱ�Ķ��ܺ�A��ʱ�Ķ�����ͬ����������A��ʼ�˶���C���������о�����·��Ϊ��������
��ͼ��ʾ���ھ�Ե�ֲ�ˮƽ���Ϸ����������㹻���ˮƽ���ҵ���ǿ�糡���������С��������һ�����ٶȴ�A�㿪ʼ��ˮƽ��������ֱ���˶�����L���ȵ���B�㣬�ٶȱ�Ϊ�㣬�˹����н�������ʧ�Ķ�����$\frac{3}{4}$ת��Ϊ�����ܣ�����������˶���ij��C��ͼ��δ�����ʱ�Ķ��ܺ�A��ʱ�Ķ�����ͬ����������A��ʼ�˶���C���������о�����·��Ϊ��������
