题目内容
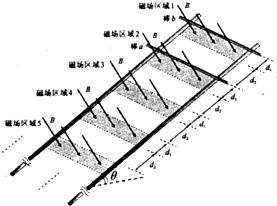 如图所示,间距为L的两条足够长的平行金属导轨与水平面的夹角为θ,导轨光滑且电阻忽略不计.场强为B的条形匀强磁场方向与导轨平面垂直,磁场区域的宽度为d1,间距为d2.两根质量均为m、有效电阻均为R的导体棒a和b放在导轨上,并与导轨垂直. (设重力加速度为g)
如图所示,间距为L的两条足够长的平行金属导轨与水平面的夹角为θ,导轨光滑且电阻忽略不计.场强为B的条形匀强磁场方向与导轨平面垂直,磁场区域的宽度为d1,间距为d2.两根质量均为m、有效电阻均为R的导体棒a和b放在导轨上,并与导轨垂直. (设重力加速度为g) (1)若a进入第2个磁场区域时,b以与a同样的速度进入第1个磁场区域,求b穿过第1个磁场区域过程中增加的动能△Ek.
(2)若a进入第2个磁场区域时,b恰好离开第1个磁场区域;此后a离开第2个磁场区域时,b 又恰好进入第2个磁场区域.且a.b在任意一个磁场区域或无磁场区域的运动时间均相.求b穿过第2个磁场区域过程中,两导体棒产生的总焦耳热Q.
(3)对于第(2)问所述的运动情况,求a穿出第k个磁场区域时的速率v.
分析:(1)a进入第2个磁场区域时,b以与a同样的速度进入第1个磁场区域时,穿过回路的磁通量不变,没有感应电流产生,两棒均不受安培力,机械能守恒,可求出△Ek.
(2)两棒分在磁场区域中和无磁场区域中运动两个过程研究:在磁场区域中,导体棒的动能和重力势能转化为内能;在无磁场区域中机械能守恒,则可根据能量守恒和机械能守恒列式求出b穿过第2个磁场区域过程中,两导体棒产生的总焦耳热Q.
(3)本问有一定的难度,由于导体棒做加速度逐渐减小的减速运动,其加速度是变化的,因此不能用匀变速运动知识解答,可以通过微积分思想进行解答,如在极短的时间内安培力可以认为不变,利用牛顿第二定律列方程,然后根据数学知识求解.
(2)两棒分在磁场区域中和无磁场区域中运动两个过程研究:在磁场区域中,导体棒的动能和重力势能转化为内能;在无磁场区域中机械能守恒,则可根据能量守恒和机械能守恒列式求出b穿过第2个磁场区域过程中,两导体棒产生的总焦耳热Q.
(3)本问有一定的难度,由于导体棒做加速度逐渐减小的减速运动,其加速度是变化的,因此不能用匀变速运动知识解答,可以通过微积分思想进行解答,如在极短的时间内安培力可以认为不变,利用牛顿第二定律列方程,然后根据数学知识求解.
解答:解:(1)a和b不受安培力作用,由机械能守恒知△Ek=mgd1sinθ①
(2)设导体棒刚进入无磁场区域时的速度为v1,刚离开无磁场区域时的速度为v2,由能量守恒知
在磁场区域中,
m
+Q=
m
+mgd1sinθ ②
在无磁场区域中
m
=
m
+mgd2sinθ ③
解得 Q=mg(d1+d2)sinθ ④
(3)在无磁场区域,根据匀变速直线运动规律有 v2-v1=gtsinθ⑤
且平均速度
=
⑥
有磁场区域,棒a受到合力 F=mgsinθ-BIl ⑦
感应电动势 ε=Blv ⑧
感应电流 I=
⑨
解得 F=mgsinθ-
v ⑩
根据牛顿第二定律得,F=ma=m
在t到t+△t时间内
(mgsinθ-
)△t=
m△v
则有mgsinθ
△t-
v△t=m
△v
解得v1-v2=gtsinθ-
d1
联立⑤⑥解得 v1=
sinθ-
由题意知v=v1=
sinθ-
答:(1)b穿过第1个磁场区域过程中增加的动能△Ek为mgd1sinθ.
(2)b穿过第2个磁场区域过程中,两导体棒产生的总焦耳热Q为mg(d1+d2)sinθ.
(3)a穿出第k个磁场区域时的速率v为
sinθ-
.
(2)设导体棒刚进入无磁场区域时的速度为v1,刚离开无磁场区域时的速度为v2,由能量守恒知
在磁场区域中,
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 2 |
在无磁场区域中
| 1 |
| 2 |
| v | 2 2 |
| 1 |
| 2 |
| v | 2 1 |
解得 Q=mg(d1+d2)sinθ ④
(3)在无磁场区域,根据匀变速直线运动规律有 v2-v1=gtsinθ⑤
且平均速度
| v1+v2 |
| 2 |
| d2 |
| t |
有磁场区域,棒a受到合力 F=mgsinθ-BIl ⑦
感应电动势 ε=Blv ⑧
感应电流 I=
| ε |
| 2R |
解得 F=mgsinθ-
| B2l2 |
| 2R |
根据牛顿第二定律得,F=ma=m
| △v |
| △t |
在t到t+△t时间内
 |
| B2l2v |
| 2R |
 |
则有mgsinθ
 |
| B2l2 |
| 2R |
 |
 |
解得v1-v2=gtsinθ-
| B2l2 |
| 2mR |
联立⑤⑥解得 v1=
| 4mgRd2 |
| B2l2d1 |
| B2l2d1 |
| 8mR |
由题意知v=v1=
| 4mgRd2 |
| B2l2d1 |
| B2l2d1 |
| 8mR |
答:(1)b穿过第1个磁场区域过程中增加的动能△Ek为mgd1sinθ.
(2)b穿过第2个磁场区域过程中,两导体棒产生的总焦耳热Q为mg(d1+d2)sinθ.
(3)a穿出第k个磁场区域时的速率v为
| 4mgRd2 |
| B2l2d1 |
| B2l2d1 |
| 8mR |
点评:注意克服安培力做功为整个回路中产生的热量;本题的难点在于第(3)问,方法巧妙,在平时练习中一定注意数学知识在物理中的应用.

练习册系列答案
相关题目
 如图所示,间距为L的光滑平行金属导轨,水平地放置在竖直方向的磁感应强度为B的匀强磁场中,一端接阻值是R的电阻.一电阻是R0,质量为m的导体棒放置在导轨上,在外力F作用下从t=0的时刻开始运动,不计导轨电阻,
如图所示,间距为L的光滑平行金属导轨,水平地放置在竖直方向的磁感应强度为B的匀强磁场中,一端接阻值是R的电阻.一电阻是R0,质量为m的导体棒放置在导轨上,在外力F作用下从t=0的时刻开始运动,不计导轨电阻,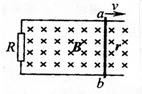 (2011?珠海一模)如图所示,间距为L的平行金属导轨上,有一电阻为r的金属棒ab与导轨接触良好.导轨左端连接电阻R,其它电阻不计,磁感应强度为B,金属捧ab以速度v向右作匀速运动,则( )
(2011?珠海一模)如图所示,间距为L的平行金属导轨上,有一电阻为r的金属棒ab与导轨接触良好.导轨左端连接电阻R,其它电阻不计,磁感应强度为B,金属捧ab以速度v向右作匀速运动,则( ) 如图所示,间距为L的两条足够长的平行金属导轨MN,PQ与水平面夹角为a,导轨的电阻不计,导轨的N、P端连接一阻值为R的电阻,导轨置于磁感应强度大小为B、方向与导轨平面垂直的匀强磁场中.将一根质量为m、电阻为r的导体棒垂直放在导轨上,导体棒ab恰能保持静止.现给导体棒一个大小为v0、方向沿导轨平面向下的初速度,然后任其运动,导体棒在运动过程中始终保持与导轨垂直并接触良好.设导体棒所受滑动摩擦力与最大静摩擦力大小相等,求:
如图所示,间距为L的两条足够长的平行金属导轨MN,PQ与水平面夹角为a,导轨的电阻不计,导轨的N、P端连接一阻值为R的电阻,导轨置于磁感应强度大小为B、方向与导轨平面垂直的匀强磁场中.将一根质量为m、电阻为r的导体棒垂直放在导轨上,导体棒ab恰能保持静止.现给导体棒一个大小为v0、方向沿导轨平面向下的初速度,然后任其运动,导体棒在运动过程中始终保持与导轨垂直并接触良好.设导体棒所受滑动摩擦力与最大静摩擦力大小相等,求: 下由静止开始运动,当cd刚要滑动时ab恰达到最大速度.(θ=30、μ=、最大静摩擦力等于滑动摩擦力)求:
下由静止开始运动,当cd刚要滑动时ab恰达到最大速度.(θ=30、μ=、最大静摩擦力等于滑动摩擦力)求: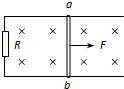 如图所示,间距为L的光滑平行金属导轨水平放置,匀强磁场的磁感应强度为B,方向垂直于导轨平面向下.导轨上有一质量为m、长为L的金属棒ab,金属棒电阻为R,导轨的一端连接阻值也为R的电阻,导轨电阻不计,金属棒ab在一水平恒力F作用下由静止开始向右运动,棒与导轨始终保持良好接触.求:
如图所示,间距为L的光滑平行金属导轨水平放置,匀强磁场的磁感应强度为B,方向垂直于导轨平面向下.导轨上有一质量为m、长为L的金属棒ab,金属棒电阻为R,导轨的一端连接阻值也为R的电阻,导轨电阻不计,金属棒ab在一水平恒力F作用下由静止开始向右运动,棒与导轨始终保持良好接触.求: