题目内容
17. 内壁光滑圆锥筒固定不动,其轴线竖直,如图,两质量相同的小球A和B紧贴内壁分别在图示所在的水平面内做匀速圆周运动,则( )
内壁光滑圆锥筒固定不动,其轴线竖直,如图,两质量相同的小球A和B紧贴内壁分别在图示所在的水平面内做匀速圆周运动,则( )| A. | A球的线速度必定大于B球的线速度 | |
| B. | A球对筒壁的压力必定大于B球对筒壁的压力 | |
| C. | A球的角速度必定小于B球的角速度 | |
| D. | A球的运动周期必定大于B球的运动周期 |
分析 对小球受力分析,受重力和支持力,合力提供向心力,根据牛顿第二定律列式求解即可分析.
解答 解:A、两球均在水平面做匀速圆周运动,由重力和筒壁的支持力的合力充当向心力,对任意一球研究,由牛顿第二定律得:
mgtanθ=m$\frac{{v}^{2}}{r}$
可得线速度 v=$\sqrt{rgtanθ}$,θ相等,A的半径大,则A的线速度大,故A正确.
B、筒壁对球的支持力 N=$\frac{mg}{cosθ}$,m、θ相等,则N相等,由牛顿第三定律知,球A对筒壁的压力一定等于球B对筒壁的压力.故B错误.
C、由mgtanθ=mω2r,得ω=$\sqrt{\frac{gtanθ}{r}}$,则知A的半径大,则A的角速度小.故C正确.
D、周期T=$\frac{2π}{ω}$,则知A的角速度小,则A的周期大.故D正确.
故选:ACD.
点评 解决本题的关键知道圆周运动向心力的来源,结合牛顿第二定律进行求解.知道线速度、角速度、周期之间的关系.

练习册系列答案
相关题目
7. 如图所示,理想变压器原、副线圈的匝数比是10:1,原线圈输入交变电压u=100$\sqrt{2}$sin50πt(V),在副线圈中接有理想电流表和定值电阻R,电容器并联在电阻R两端,电阻阻值R=10Ω,关于电路分析,下列说法中正确的是( )
如图所示,理想变压器原、副线圈的匝数比是10:1,原线圈输入交变电压u=100$\sqrt{2}$sin50πt(V),在副线圈中接有理想电流表和定值电阻R,电容器并联在电阻R两端,电阻阻值R=10Ω,关于电路分析,下列说法中正确的是( )
 如图所示,理想变压器原、副线圈的匝数比是10:1,原线圈输入交变电压u=100$\sqrt{2}$sin50πt(V),在副线圈中接有理想电流表和定值电阻R,电容器并联在电阻R两端,电阻阻值R=10Ω,关于电路分析,下列说法中正确的是( )
如图所示,理想变压器原、副线圈的匝数比是10:1,原线圈输入交变电压u=100$\sqrt{2}$sin50πt(V),在副线圈中接有理想电流表和定值电阻R,电容器并联在电阻R两端,电阻阻值R=10Ω,关于电路分析,下列说法中正确的是( )| A. | 电流表示数是1A | B. | 电流表示数是0.5A | ||
| C. | 电阻R消耗的电功率为10W | D. | 电容器的耐压值至少是10V |
2.下列说法正确的是( )
| A. | 一群氢原子从n=4的能级跃迁只能辐射5种频率的光子 | |
| B. | ${\;}_{83}^{210}$Bi衰变${\;}_{84}^{210}$Po要释放β粒子 | |
| C. | 质量为m的铀元素经过3个半衰期后质量变成$\frac{1}{8}$m | |
| D. | 氢原子从激发态跃迁到基态,则核外电子电势能减少,动能增大 | |
| E. | 用不可见光照射金属一定比用可见光照射同种金属产生的光电子的初动能大 |
9. 2014年10月24日,“嫦娥五号”在西昌卫星发射中心发射升空,并在8天后以“跳跃式再入”方式成功返回地面.“跳跃式再入”指航天器在关闭发动机后进入大气层,依靠大气升力再次冲出大气层,降低速度后在进入大气层,如图所示,虚线为大气层的边界(虚线圆的圆心为地心).已知地球半径R,地心到d点的距离为r,地球表面重力加速度为g.关于“嫦娥五号”,下列说法正确的是( )
2014年10月24日,“嫦娥五号”在西昌卫星发射中心发射升空,并在8天后以“跳跃式再入”方式成功返回地面.“跳跃式再入”指航天器在关闭发动机后进入大气层,依靠大气升力再次冲出大气层,降低速度后在进入大气层,如图所示,虚线为大气层的边界(虚线圆的圆心为地心).已知地球半径R,地心到d点的距离为r,地球表面重力加速度为g.关于“嫦娥五号”,下列说法正确的是( )
 2014年10月24日,“嫦娥五号”在西昌卫星发射中心发射升空,并在8天后以“跳跃式再入”方式成功返回地面.“跳跃式再入”指航天器在关闭发动机后进入大气层,依靠大气升力再次冲出大气层,降低速度后在进入大气层,如图所示,虚线为大气层的边界(虚线圆的圆心为地心).已知地球半径R,地心到d点的距离为r,地球表面重力加速度为g.关于“嫦娥五号”,下列说法正确的是( )
2014年10月24日,“嫦娥五号”在西昌卫星发射中心发射升空,并在8天后以“跳跃式再入”方式成功返回地面.“跳跃式再入”指航天器在关闭发动机后进入大气层,依靠大气升力再次冲出大气层,降低速度后在进入大气层,如图所示,虚线为大气层的边界(虚线圆的圆心为地心).已知地球半径R,地心到d点的距离为r,地球表面重力加速度为g.关于“嫦娥五号”,下列说法正确的是( )| A. | 在b点处于完全失重状态 | B. | 在b点所受合外力为零 | ||
| C. | 在d点的加速度小于$\frac{g{R}^{2}}{{r}^{2}}$ | D. | 在d点的加速度等于$\frac{g{R}^{2}}{{r}^{2}}$ |
12.某人造卫星绕地球做匀速圆周运动,其轨道半径是月球轨道半径的$\frac{1}{4}$,则此卫星运动的周期大约是( )
| A. | 1天~5天 | B. | 5天~10天 | C. | 10天~15天 | D. | 15天~20天 |

 如图所示,在以原点O为圆心、半径为R的半圆形区域内充满了磁感应强度为B的匀强磁场,x轴下方为一平行板电容器,其正极板与x轴重合且在O处开有小孔,两极板间距离为$\frac{πR}{12}$.现有电荷量为e、质量为m的电子在O点正下方负极板上的P点由静止释放.不计电子所受重力.
如图所示,在以原点O为圆心、半径为R的半圆形区域内充满了磁感应强度为B的匀强磁场,x轴下方为一平行板电容器,其正极板与x轴重合且在O处开有小孔,两极板间距离为$\frac{πR}{12}$.现有电荷量为e、质量为m的电子在O点正下方负极板上的P点由静止释放.不计电子所受重力.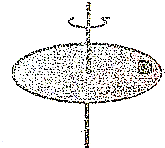 如图所示,质量为m的物体放在粗糙的水平转盘上,物体到转盘轴的距离为r,物体与转盘间的动摩擦因数为μ,现让转盘的转速由0逐渐增大,直到物体恰好不滑离转盘为止.求:
如图所示,质量为m的物体放在粗糙的水平转盘上,物体到转盘轴的距离为r,物体与转盘间的动摩擦因数为μ,现让转盘的转速由0逐渐增大,直到物体恰好不滑离转盘为止.求: