(选修3-5)
(1)核能是一种高效的能源.
①在核电站中,为了防止放射性物质泄漏,核反应堆有三道防护屏障:燃料包壳,压力壳和安全壳(见图甲).结合图乙可知,安全壳应当选用的材料是
混凝土
混凝土
.
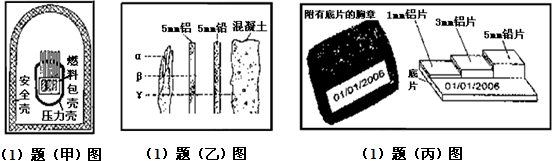
②图丙是用来监测工作人员受到辐射情况的胸章,通过照相底片被射线感光的区域,可以判断工作人员受到何种辐射.当胸章上1mm铝片和3mm铝片下的照相底片被感光,而铅片下的照相底片未被感光时,结合图2分析工作人员受到了
β
β
射线的辐射;当所有照相底片被感光时,工作人员受到了
γ
γ
射线的辐射.
(2)下列说法正确的是
A.卢瑟福的a粒子散射实验揭示了原子核有复杂的结构
B.受普朗克量子论的启发,爱因斯坦在对光电效应的研究中,提出了光子说
C.核反应方程
U→
Th+
He属于裂变
D.宏观物体的物质波波长非常小,极易观察到它的波动性
E.根据爱因斯坦质能方程,物体具有的能量和它的质量之间存在着正比关系
F.β衰变中产生的β射线实际上是原子的核外电子挣脱原子核的束缚而形成的
G.中子与质子结合成氘核的过程中需要吸收能量
H.升高放射性物质的温度,可缩短其半衰期
I.氢原子辐射出一个光子后,根据玻尔理论可知氢原子的电势能增大,核外电子的运动加速度增大
J.对于任何一种金属都存在一个“最大波长”,入射光的波长必须小于这个波长,才能产生光电效应
(3)如图所示,质量为M=2kg的足够长的小平板车静止在光滑水平面上,车的一端静止着质量为M
A=2kg的物体A(可视为质点).一个质量为m=20g的子弹以500m/s的水平速度迅即射穿A后,速度变为100m/s,最后物体A静止在车上.若物体A与小车间的动摩擦因数μ=0.5.(g取10m/s
2)

①平板车最后的速度是多大?
②全过程损失的机械能为多少?
③A在平板车上滑行的距离为多少?
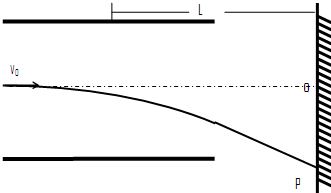 如图所示,质量为m,电量为q的带电粒子以初速v0进入由两个平行金属板构成的场强为E的匀强电场中,两极板长度为L,电容器极板中央到光屏的距离也是L.已知带电粒子打到光屏的P点,不计重力作用.求偏移量OP的大小.
如图所示,质量为m,电量为q的带电粒子以初速v0进入由两个平行金属板构成的场强为E的匀强电场中,两极板长度为L,电容器极板中央到光屏的距离也是L.已知带电粒子打到光屏的P点,不计重力作用.求偏移量OP的大小.
 如图所示,质量为m的球,被长为L的细绳吊起处于静止状态.现对小球施加水平向右的恒力F,小球开始向右运动,当细绳与竖直方向的夹角为60°,小球速度恰好为0( )
如图所示,质量为m的球,被长为L的细绳吊起处于静止状态.现对小球施加水平向右的恒力F,小球开始向右运动,当细绳与竖直方向的夹角为60°,小球速度恰好为0( )

 (2010?黑龙江模拟)(按题目要求作答,写出必要的文字说明、方程式和重要演算步骤,只写出最后答案不得分)
(2010?黑龙江模拟)(按题目要求作答,写出必要的文字说明、方程式和重要演算步骤,只写出最后答案不得分) (2005?青浦区模拟)如图所示,质量为m的带电金属小球,用绝缘细线与质量为M(M=2m)的不带电木球相连,两球恰能在竖直向上的足够大且场强为E的匀强电场中,以速度v匀速竖直向上运动,当木球升至a点时,细线突然断裂,木球升至b点时速度为零.则木球速度为零时,金属球的速度大小为
(2005?青浦区模拟)如图所示,质量为m的带电金属小球,用绝缘细线与质量为M(M=2m)的不带电木球相连,两球恰能在竖直向上的足够大且场强为E的匀强电场中,以速度v匀速竖直向上运动,当木球升至a点时,细线突然断裂,木球升至b点时速度为零.则木球速度为零时,金属球的速度大小为 (2003?徐州一模)如图所示,质量为M的木板可以沿倾角为α的固定斜面无摩擦地滑下,欲使木板静止在斜面上,木板上质量为m的人应以多大的加速度向下奔跑?
(2003?徐州一模)如图所示,质量为M的木板可以沿倾角为α的固定斜面无摩擦地滑下,欲使木板静止在斜面上,木板上质量为m的人应以多大的加速度向下奔跑?