题目内容
【题目】如图所示,矩形区域ABCD处在与其所在平面垂直的匀强磁场中,磁感应强度B0,方向向里,AB=3L,BC=L,E、F为AB、CD的三等分点,AE段为电子发射源,CF段固定有电子收集板,设电子质量为m,电量为e,大量电子以相同初动能垂直AE飞出,取![]() ,求:
,求:

(1)电子初动能取何值,AE段发射的电子经磁场偏转后全部被收集板吸收;
(2)初动能满足什么条件收集板一定能收集到电子;
(3)初动能取何值,有电子以最短时间击中收集板,最短时间为多少。
【答案】(1) ![]() (2)
(2) ![]() (3)
(3) ![]()

【解析】(1)由于所有电子半径相同,要是AE段发射的电子经磁场偏转后全部被收集板吸收,那么就要保证A点发出的电子经过磁场偏转后能打在F点,如图所示:

由几何关系得: ![]()
![]()
则半径: ![]()
粒子旋转时洛伦兹力提供向心力,则![]()
粒子的动能为![]()
(2)画出电子运动的半径与边界的关系如图所示:
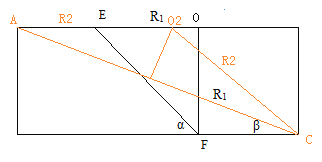
半径最小时,则E点发射的打在F点, 由图可知此时![]()
![]() 得动能:
得动能: ![]()
半径最大时:则A点发射的电子打到C点,由图可知: ![]()
![]() 得动能
得动能![]()
所以要是收集板上有电子则动能的取值范围![]()
(3)要是运动的时间最短,则要保证圆心角最小,则弦切角最小,则从A到C运动的电子对应的圆心角最小,由上图可知:圆心角![]() ,而
,而![]()
则![]() 得:
得: ![]()
所以电子在磁场中运动的最短时间: 
则A点发射的电子打到C点,由图可知:
![]() 得动能
得动能![]()
综上所述本题答案是:(1) ![]() (2)
(2) ![]() (3)
(3) ![]()


练习册系列答案
相关题目









