题目内容
(16分)如图所示,在半径为 的圆形区域内有水平向里的匀强磁场,磁感应强度B,圆形区域右侧有一竖直感光板,从圆弧顶点P以速率
的圆形区域内有水平向里的匀强磁场,磁感应强度B,圆形区域右侧有一竖直感光板,从圆弧顶点P以速率 的带正电粒子平行于纸面进入磁场,已知粒子的质量为m,电量为q,粒子重力不计。
的带正电粒子平行于纸面进入磁场,已知粒子的质量为m,电量为q,粒子重力不计。

⑴若粒子对准圆心射入,求它在磁场中运动的时间;
⑵若粒子对准圆心射入,且速率为
 ,求它打到感光板上时速度的垂直分量;
,求它打到感光板上时速度的垂直分量;
⑶若粒子以速度 从P点以任意角入射,试证明它离开磁场后均垂直打在感光板上。
从P点以任意角入射,试证明它离开磁场后均垂直打在感光板上。
 的圆形区域内有水平向里的匀强磁场,磁感应强度B,圆形区域右侧有一竖直感光板,从圆弧顶点P以速率
的圆形区域内有水平向里的匀强磁场,磁感应强度B,圆形区域右侧有一竖直感光板,从圆弧顶点P以速率 的带正电粒子平行于纸面进入磁场,已知粒子的质量为m,电量为q,粒子重力不计。
的带正电粒子平行于纸面进入磁场,已知粒子的质量为m,电量为q,粒子重力不计。
⑴若粒子对准圆心射入,求它在磁场中运动的时间;
⑵若粒子对准圆心射入,且速率为

 ,求它打到感光板上时速度的垂直分量;
,求它打到感光板上时速度的垂直分量;⑶若粒子以速度
 从P点以任意角入射,试证明它离开磁场后均垂直打在感光板上。
从P点以任意角入射,试证明它离开磁场后均垂直打在感光板上。(1)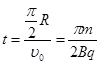 (2)
(2)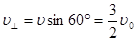 (3)证明过程见答案
(3)证明过程见答案
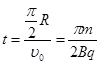 (2)
(2)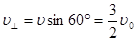 (3)证明过程见答案
(3)证明过程见答案试题分析:(1)设带电粒子进入磁场中做匀速圆周运动的轨道半径为
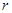 ,由牛顿第二定律得
,由牛顿第二定律得
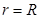
带电粒子在磁场中的运动轨迹为四分之一圆周,轨迹对应的圆心角为
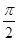 ,如图所示,则
,如图所示,则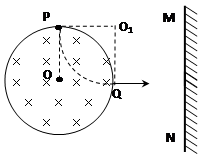
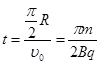
(2)由(1)知,当
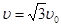 时,带电粒子在磁场中运动的轨道半径为
时,带电粒子在磁场中运动的轨道半径为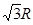
其运动轨迹如图所示,
由图可知
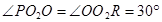
所以带电粒子离开磁场时偏转原来方向60°
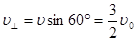
(3)由(1)知,当带电粒子以
 射入时,带电粒子在磁场中的运动轨道半径为R。
射入时,带电粒子在磁场中的运动轨道半径为R。设粒子射入方向与PO方向夹角为
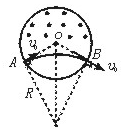
 ,带电粒子从区域边界S射出,带电粒子运动轨迹如图所示。
,带电粒子从区域边界S射出,带电粒子运动轨迹如图所示。
因PO3=O3S=PO=SO=R
所以四边形POSO3为棱形
由图可知:
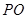 ∥
∥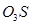 ,
,  ⊥SO3
⊥SO3因此,带电粒子射出磁场时的方向为水平方向,与入射的方向无关。
点评:此类题型考察了带电粒子在磁场中的偏转,涉及到偏转圆心角以及根据几何关系确定半径大小。这类问题的解决关键通常是确定圆心以及轨迹

练习册系列答案
相关题目

 延长线的夹角为30°.粒子在这过程中只受磁场力的作用。
延长线的夹角为30°.粒子在这过程中只受磁场力的作用。
 πr/3v0
πr/3v0
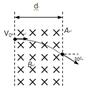

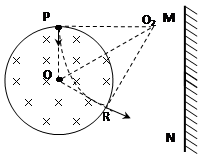
 , OA、OB将xOy平面分为Ⅰ、Ⅱ、Ⅲ三个区域,区域Ⅰ、Ⅲ内存在水平方向的匀强电场,电场强度大小相等、方向相反。带电粒子自x轴上的粒子源P处以速度v0沿y轴正方向射出,经时间t到达OA上的M点,且此时速度与OA垂直。已知M到原点O的距离OM = a,不计粒子的重力。求:
, OA、OB将xOy平面分为Ⅰ、Ⅱ、Ⅲ三个区域,区域Ⅰ、Ⅲ内存在水平方向的匀强电场,电场强度大小相等、方向相反。带电粒子自x轴上的粒子源P处以速度v0沿y轴正方向射出,经时间t到达OA上的M点,且此时速度与OA垂直。已知M到原点O的距离OM = a,不计粒子的重力。求: ,但速度大小均相同,如图所示,求所有粒子经过OB时的区域长度。
,但速度大小均相同,如图所示,求所有粒子经过OB时的区域长度。
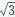 d),在原点O和Q处分别固定一个垂直于y轴的较小的弹性挡板,当粒子与挡板碰撞后在平行于挡板的方向上速度不变,在垂直于挡板的方向上速度大小不变、方向与原方向相反。一质量为m、电荷量为q的带正电粒子(重力不计)从P点沿垂直于x轴的方向进入第二象限内,在x轴上方运动半周后进入x轴下方,若粒子又能返回P点,试求:
d),在原点O和Q处分别固定一个垂直于y轴的较小的弹性挡板,当粒子与挡板碰撞后在平行于挡板的方向上速度不变,在垂直于挡板的方向上速度大小不变、方向与原方向相反。一质量为m、电荷量为q的带正电粒子(重力不计)从P点沿垂直于x轴的方向进入第二象限内,在x轴上方运动半周后进入x轴下方,若粒子又能返回P点,试求: