��Ŀ����
����Ŀ����ͼ��ʾ��M��NΪ��ֱ���õ�ƽ�н����壬��������ӵ�ѹΪU0��S1��S2Ϊ�������Ե�С�ס�������P��Qˮƽ������N���Ҳ࣬����С��S1��S2����ֱ�߶Գƣ�����ij��Ⱥ������ľ����Ϊl���������P��Q�ұ�Եl����һӫ������ӫ������ֱ�ڽ�����P��Q��ȡ������S1��S2���ߵ�O��Ϊԭ�㣬����Ϊ��������x�ᡣM��������ǹ������ĵ��Ӿ�С��S1����M��N����䡣���ӵ�����Ϊm�������Ϊe�����ٶȿ��Ժ��ԡ����Ƶ��������͵���֮�������á�

��1������ӵ���С��S2ʱ���ٶȴ�Сv��
��2������P��Q��ֻ���ڴ�ֱ��ֽ���������ǿ�ų������Ӹպþ���P����ұ�Ե����ӫ�����ϡ���ų��ĴŸ�Ӧǿ�ȴ�СB�͵��Ӵ���ӫ�����ϵ�λ������x��
��3����������P��Q��ֻ���ڵ糡��P��Q������ѹu��ʱ��t�ı仯��ϵ��ͼ��ʾ����λʱ���ڴ�С��S1����ĵ��Ӹ���ΪN�����Ӵ���ӫ�������γ�һ�����ߡ����Ե糡�仯�����Ĵų���������Ϊÿ�������ڰ�P��Q���˶������У������ĵ�ѹ�㶨������2t0ʱ���ڴ�λ���������ϵĵ��Ӹ���n��
���𰸡���1��![]() ��2��
��2��![]() ��3��
��3��![]()
����������1�����ݶ��ܶ��� ![]()
��ã�![]()
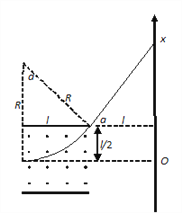
��2�������ڴų���������Բ���˶�����Բ�˶��뾶Ϊ R��
�ɼ��ι�ϵ![]() �ã�
�ã�![]()
����ţ�ٵڶ����ɣ�![]() �ã�
�ã�![]()
��Բ������Բ��Ϊ�������㣺![]() ��
��![]()
�����뿪�ų����������˶� ![]()
�������![]()
��3���� �������ƫת�糡PQ�е��˶�ʱ��Ϊt1��PQ��ĵ�ѹΪu
��ֱ�糡����l=vt1 ƽ�е糡����![]()
���ٶ�![]()
�ã�![]()
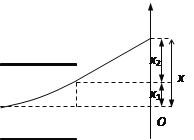
���ӳ�ƫת�糡ʱ����x������ٶ� vx=at1
������ƫת�糡��������ֱ���˶����辭ʱ��t2����ӫ��������ˮƽ����l=vt2
��ֱ������x2=vxt2 ��ã�![]()
���Ӵ���ӫ�����ϵ�λ������ ![]()
����ͼ��֪��������tʱ���ڣ�P��Q���ѹ�仯u��ȡ�
��֪������ӫ�����ϵĵ����γɵ����߳���![]()
���ԣ�������tʱ���ڣ����߳���x���,��һ�������ڵ�λ���������ϵĵ��Ӹ�����ͬ��
����2t0ʱ���ڴ�λ���������ϵĵ��Ӹ������������ڵ糡�еIJ�����Ϊx1=![]() ʱ����
ʱ���� ![]()
�ã�u=2U0
��ƫת��ѹ��0~��2U0֮��ʱ������P��Q��ĵ��ӿɴ���ӫ�����ϡ�
��ͼ��֪��һ�������ڵ����ܴ�P��Q�糡�����ʱ��![]()
һ�������ڴ���ӫ�����ϵĵ�����![]()
����![]() �ã����Ӵ���ӫ�����ϵ���������
�ã����Ӵ���ӫ�����ϵ���������![]()
���߳���L=2xm=3l ���ԣ���0~2t0ʱ���ڣ���λ���������ϵĵ�����![]()

 ������������Ӧ����ϵ�д�
������������Ӧ����ϵ�д� ͬ����չ�Ķ�ϵ�д�
ͬ����չ�Ķ�ϵ�д�







