题目内容
5. 如图所示,A、B两球用两段不可伸长的细线连接于悬点0,两段细绳的长度之比为1:2,现让两球同时从悬点O以一定的初速度分别向左、向右水平抛出,至连接两球的细绳伸直所用时间之比为1:$\sqrt{2}$,若两球的初速度之比$\frac{{v}_{A}}{{v}_{B}}$为k,则k值应满足的条件是( )
如图所示,A、B两球用两段不可伸长的细线连接于悬点0,两段细绳的长度之比为1:2,现让两球同时从悬点O以一定的初速度分别向左、向右水平抛出,至连接两球的细绳伸直所用时间之比为1:$\sqrt{2}$,若两球的初速度之比$\frac{{v}_{A}}{{v}_{B}}$为k,则k值应满足的条件是( )| A. | k=$\frac{1}{\sqrt{2}}$ | B. | k>$\frac{1}{\sqrt{2}}$ | C. | k=$\frac{1}{2}$ | D. | k>$\frac{1}{2\sqrt{2}}$ |
分析 两个小球同时从悬点O附近以一定的初速度分别向左、向右水平抛出,当绳子被拉直时,合位移之间的关系等于绳子长度的关系,可以根据几何关系求出相应的物理量.
解答 解:设连接A球的绳长为L,以速度vA水平抛出,x=vAt,$y=\frac{1}{2}g{t}^{2}$,x2+y2=L2,
得:${v}_{A}=\frac{\sqrt{{L}^{2}-(\frac{1}{2}g{t}^{2})^{2}}}{t}$,
同理得${v}_{B}=\frac{\sqrt{{(2L)}^{2}-{[\frac{1}{2}g{(\sqrt{2}t)}^{2}]}^{2}}}{\sqrt{2}t}$=$\frac{2\sqrt{{L}^{2}-{(\frac{1}{2}g{t}^{2})}^{2}}}{\sqrt{2}t}$,
因此有:$\frac{{v}_{A}}{{v}_{B}}=k=\frac{1}{\sqrt{2}}$,故A项正确.
故选:A
点评 本题考查了平抛运动的基本概念和基本公式,题目中对几何知识的要求比较高,属于中档题.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
15. 我国自主研制的高分辨率对地观测系统包含至少7颗卫星和其他观测平台,分别编号为“高分一号”到“高分七号”,它们都将在2020年前发射并投入使用.于2013年4月发射成功的“高分一号”是一颗低轨遥感卫星,其轨道高度为645km.关于“高分一号”卫星,下列说法正确的是( )
我国自主研制的高分辨率对地观测系统包含至少7颗卫星和其他观测平台,分别编号为“高分一号”到“高分七号”,它们都将在2020年前发射并投入使用.于2013年4月发射成功的“高分一号”是一颗低轨遥感卫星,其轨道高度为645km.关于“高分一号”卫星,下列说法正确的是( )
 我国自主研制的高分辨率对地观测系统包含至少7颗卫星和其他观测平台,分别编号为“高分一号”到“高分七号”,它们都将在2020年前发射并投入使用.于2013年4月发射成功的“高分一号”是一颗低轨遥感卫星,其轨道高度为645km.关于“高分一号”卫星,下列说法正确的是( )
我国自主研制的高分辨率对地观测系统包含至少7颗卫星和其他观测平台,分别编号为“高分一号”到“高分七号”,它们都将在2020年前发射并投入使用.于2013年4月发射成功的“高分一号”是一颗低轨遥感卫星,其轨道高度为645km.关于“高分一号”卫星,下列说法正确的是( )| A. | 发射速度一定大于7.9km/s | |
| B. | 可以定点在相对地面静止的同步轨道上 | |
| C. | 卫星绕地球运行的线速度比月球的大 | |
| D. | 卫星绕地球运行的周期比月球的小 |
16.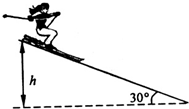 如图所示,某段滑雪道倾角为30°,总质量为m(包括雪具在内)的滑雪运动员从雪上距底端高为h处由静止开始匀加速下滑,加速度大小为$\frac{1}{3}$g,他沿雪道滑到底端的过中,下列说法正确的是( )
如图所示,某段滑雪道倾角为30°,总质量为m(包括雪具在内)的滑雪运动员从雪上距底端高为h处由静止开始匀加速下滑,加速度大小为$\frac{1}{3}$g,他沿雪道滑到底端的过中,下列说法正确的是( )
 如图所示,某段滑雪道倾角为30°,总质量为m(包括雪具在内)的滑雪运动员从雪上距底端高为h处由静止开始匀加速下滑,加速度大小为$\frac{1}{3}$g,他沿雪道滑到底端的过中,下列说法正确的是( )
如图所示,某段滑雪道倾角为30°,总质量为m(包括雪具在内)的滑雪运动员从雪上距底端高为h处由静止开始匀加速下滑,加速度大小为$\frac{1}{3}$g,他沿雪道滑到底端的过中,下列说法正确的是( )| A. | 运动员减少的重力势能全部转化为动能 | |
| B. | 运动员获得的动能为mgh | |
| C. | 运动员克服摩擦力做功为$\frac{2}{3}$mgh | |
| D. | 运动员减少的机械能为$\frac{1}{3}$mgh |
13.火车以速度v1匀速行驶,司机发现前方同轨道上相距s处有另一火车沿同方向以速度v2(对地且v1>v2) 做匀速直线运动.司机立即以加速度a紧急刹车.要使两车不相撞,a应满足什么条件?( )
| A. | a≥$\frac{{{v_1}^2-{v_2}^2}}{2s}$ | B. | a≤$\frac{{{v_1}^2-{v_2}^2}}{2s}$ | C. | a≥$\frac{{{{({v_1}-{v_2})}^2}}}{2s}$ | D. | a≤$\frac{{{{({v_1}-{v_2})}^2}}}{2s}$ |
20. 如图所示,直线Ⅰ、Ⅱ分别是电源1与电源2的路端电压随输出电流变化的特性图线,曲线Ⅲ是一个小灯泡的伏安特性曲线,如果把该小灯泡先后分别与电源1和电源2单独连接时,则下列说法不正确的是( )
如图所示,直线Ⅰ、Ⅱ分别是电源1与电源2的路端电压随输出电流变化的特性图线,曲线Ⅲ是一个小灯泡的伏安特性曲线,如果把该小灯泡先后分别与电源1和电源2单独连接时,则下列说法不正确的是( )
 如图所示,直线Ⅰ、Ⅱ分别是电源1与电源2的路端电压随输出电流变化的特性图线,曲线Ⅲ是一个小灯泡的伏安特性曲线,如果把该小灯泡先后分别与电源1和电源2单独连接时,则下列说法不正确的是( )
如图所示,直线Ⅰ、Ⅱ分别是电源1与电源2的路端电压随输出电流变化的特性图线,曲线Ⅲ是一个小灯泡的伏安特性曲线,如果把该小灯泡先后分别与电源1和电源2单独连接时,则下列说法不正确的是( )| A. | 电源1和电源2的内阻之比是7:5 | |
| B. | 在这两种连接状态下,小灯泡的电阻之比是16:21 | |
| C. | 在这两种连接状态下,电源的输出功率之比是3:2 | |
| D. | 在这两种连接状态下,电源的输出功率之比是7:12 |
10. 如图所示,平行板电容器与直流电源、理想二极管(正向电阻为零可以视为短路,反响电阻无穷大可以视为断路)连接,电源负极接地.初始电容器不带电,闭合开关稳定后,一带电油滴位于容器中的P点且处于静止状态.下列说法正确的是( )
如图所示,平行板电容器与直流电源、理想二极管(正向电阻为零可以视为短路,反响电阻无穷大可以视为断路)连接,电源负极接地.初始电容器不带电,闭合开关稳定后,一带电油滴位于容器中的P点且处于静止状态.下列说法正确的是( )
 如图所示,平行板电容器与直流电源、理想二极管(正向电阻为零可以视为短路,反响电阻无穷大可以视为断路)连接,电源负极接地.初始电容器不带电,闭合开关稳定后,一带电油滴位于容器中的P点且处于静止状态.下列说法正确的是( )
如图所示,平行板电容器与直流电源、理想二极管(正向电阻为零可以视为短路,反响电阻无穷大可以视为断路)连接,电源负极接地.初始电容器不带电,闭合开关稳定后,一带电油滴位于容器中的P点且处于静止状态.下列说法正确的是( )| A. | 减小极板间的正对面积,带电油滴会向上移动,且P点的电势会降低 | |
| B. | 将上极板下移,则P点的电势不变 | |
| C. | 将下极板下移,则P点的电势升高 | |
| D. | 无论哪个极板上移还是下移,带电油滴都不可能向下运动 |
17.用材料和粗细相同、长短不同的两段绳子,各拴一个质量相同的小球在光滑水平面上做匀速圆周运动,那么以下说法错误的是( )
| A. | 两个球以相同的线速度运动时,短绳易断 | |
| B. | 两个球以相同的角速度运动时,长绳易断 | |
| C. | 两个球以相同的周期运动时,长绳易断 | |
| D. | 两个小球以相同大小的加速度运动时,短绳易断. |
14.一物体做匀变速直线运动,下列说法中正确的是( )
| A. | 物体的末速度一定与时间成正比 | |
| B. | 物体的位移一定与时间的平方成正比 | |
| C. | 物体的速度在一定时间内发生的变化与这段时间成正比 | |
| D. | 若物体做匀加速直线运动,则速度和位移都随时间增大;若物体做匀减速直线运动,则速度和位移都随时间减小 |
15.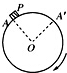 如图所示,在圆柱体上放一物块P,圆柱体绕水平轴O缓慢转动,在物块从A转至A′的过程中,物块与圆柱体保持相对静止,下列说法正确的是( )
如图所示,在圆柱体上放一物块P,圆柱体绕水平轴O缓慢转动,在物块从A转至A′的过程中,物块与圆柱体保持相对静止,下列说法正确的是( )
 如图所示,在圆柱体上放一物块P,圆柱体绕水平轴O缓慢转动,在物块从A转至A′的过程中,物块与圆柱体保持相对静止,下列说法正确的是( )
如图所示,在圆柱体上放一物块P,圆柱体绕水平轴O缓慢转动,在物块从A转至A′的过程中,物块与圆柱体保持相对静止,下列说法正确的是( )| A. | 物块P所受支持力先减小后增大 | B. | 物块P所受支持力先增大后减小 | ||
| C. | 物块P所受摩擦力先减小后增大 | D. | 物块P所受摩擦力先增大后减小 |