题目内容
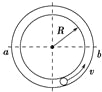
【题目】如图所示，光滑水平面左侧固定一竖直弹性挡板，右侧固定一内壁光滑的竖直圆形轨道，轨道下端与地面相切于d点，且切点处略微错开．水平轨道上a、b、c、d间的距离ab=bc=cd，P、Q两物体之间压缩一段轻弹簧（两物体未与弹簧两端连接），并通过一细线约束，静止在b、c两点，此时弹簧储存的弹性势能为Ep=10J．现剪断细线，当弹簧恢复原长时立即撤走弹簧，当Q首次运动到d点时，P恰好追上Q，并与之发生碰撞，碰后粘在一起，接着进入竖直平面的圆轨道．已知P的质量mP=1 kg，P、Q两物体均可以视为质点，不计P与左侧竖直挡板碰撞的时间，P到达a前与Q到达d前弹簧已恢复原长．求：
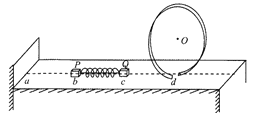
（1）物体Q的质量；
（2）若P、Q两物体碰后在圆形轨道内运动时不脱离轨道，轨道半径应该满足什么条件？
【答案】（1）4kg（2）R≥0.128m或R≤0.0512m
【解析】试题分析：释放弹簧过程系统动量守恒，弹簧恢复原长后两物体均做匀速直线运动，应用动量守恒定律求出物体Q的质量．由动量守恒定律与能量守恒定律求出P、Q的速度，应用机械能守恒定律与牛顿第二定律求出PQ不脱离圆轨道的临界半径，然后答题．
试题分析：（1）释放弹簧过程系统动量守恒，以向右为正方向，
由动量守恒定律得： 
，则
，
两物体运动时间t相等，则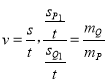
，即
，
弹簧恢复原长后两物体均做匀速直线运动，运动时间相等，则： 
，
从剪断细线到P追上Q过程， 
，由题意可知： 
，
则： 
，解得
；
（2）释放弹簧过程系统动量守恒，以向右为正方向，
由动量守恒定律得： 
，
由机械能守恒定律得： 
，解得
，
P、Q碰撞过程系统动量守恒，以向右为正方向，
由动量守恒定律得
，解得： 
；
①PQ恰好到达与O点等高处，由机械能守恒定律得： 
，
解得：R=0.128m，要使P、Q不脱离轨道： 
；
②P、Q恰好能够通过圆形轨道最高点，在最高点，
由动能定理得
，
从圆形轨道最低点到最高点过程，由机械化守恒定律得： 
，
解得： 
，
PQ不脱离圆轨道： 
；
综上所述若P、Q两物体碰后在圆形轨道内运动时不脱离轨道，轨道半径应该满足的条件是
或
．
