题目内容
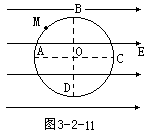
如图15所示，水平绝缘轨道AB与处于竖直平面内的半圆形绝缘光滑轨道BC平滑连接，半圆形轨道的半径R=0.40m。轨道所在空间存在水平向右的匀强电场，电场强度E=1.0×104 N/C。现有一电荷量q=+1.0×10-4C，质量m=0.10 kg的带电体（可视为质点），在水平轨道上的P点由静止释放，带电体运动到圆形轨道最低点B时的速度vB=5.0m/s。已知带电体与水平轨道间的动摩擦因数μ=0.50，重力加速度g=10m/s2。求：
（1）带电体运动到圆形轨道的最低点B时，圆形轨道对带电体支持力的大小；
（2）带电体在水平轨道上的释放点P到B点的距离；
（3）带电体第一次经过C点后，落在水平轨道上的位置到B点的距离。
（1）带电体运动到圆形轨道的最低点B时，圆形轨道对带电体支持力的大小；
（2）带电体在水平轨道上的释放点P到B点的距离；
（3）带电体第一次经过C点后，落在水平轨道上的位置到B点的距离。
（1）7.25 N（2）2.5 m（3）0.40m
（1）设带电体在B点受到的支持力为FN，依据牛顿第二定律
FN-mg=m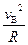
.................................................3分
解得FN="7.25" N…..................................................2分
（2）设PB间的距离为s，依据动能定理
(qE-mmg)s=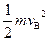
……..…............................ ........3分
解得s="2.5" m ……..….. .............................….........…2分
（3）设带电体运动到C点的速度为vC，依据机械能守恒定律
=
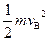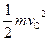+2mgR........................…………….…….….…...…1分
带电体离开C点后在竖直方向上做自由落体运动，设在空间运动的时间为t
2R=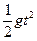
.................................................1分
在水平方向上做匀减速运动，设在水平方向的加速度大小为a，依据牛顿第二定律
qE=ma................................... 1分
设落在水平轨道上的位置到B点的距离为x，依据运动学公式
x=vct-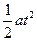
..................................1分
解得 x=0.40m.................................. 2分
FN-mg=m
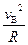.................................................3分解得FN="7.25" N…..................................................2分
（2）设PB间的距离为s，依据动能定理
(qE-mmg)s=
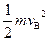……..…............................ ........3分解得s="2.5" m ……..….. .............................….........…2分
（3）设带电体运动到C点的速度为vC，依据机械能守恒定律
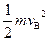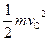=+2mgR........................…………….…….….…...…1分带电体离开C点后在竖直方向上做自由落体运动，设在空间运动的时间为t
2R=
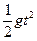.................................................1分在水平方向上做匀减速运动，设在水平方向的加速度大小为a，依据牛顿第二定律
qE=ma................................... 1分
设落在水平轨道上的位置到B点的距离为x，依据运动学公式
x=vct-
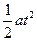..................................1分解得 x=0.40m.................................. 2分
练习册系列答案
特高级教师点拨系列答案
相关题目
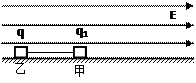
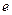=1.6×10
C，质量
=0.91×10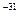
kg，电子所受重力及电子之间的相互作用力均可忽略不计，不考虑相对论效应。
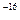J，求加速电压
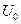为多大；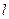
=4.0cm，两板间距离
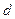=1.0cm，极板右端与荧光屏的距离
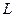=18cm，当在偏转电极上加
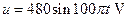的正弦交变电压时，如果电子进入偏转电场的初速度
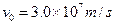，求电子打在荧光屏上产生亮线的最大长度；
、
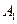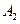和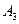
三个阳极除了对电子加速外，还共同完成对电子的聚焦作用，其中聚焦电场可简化为如图14丁所示的电场，图中的虚线是该电场的等势线。请简要说明聚焦电场如何实现对电子的聚焦作用。