题目内容
如图所示,在方向水平向右、大小为E=6×103N/C的匀强电场中有一个光滑的绝缘平面。一根绝缘细绳两端分别系有带电滑块甲和乙,甲的质量为m1=2×10-4kg,带电量为q1=2×10-9C,乙的质量为m2=1×10-4kg,带电量为q2=-1×10-9C。开始时细绳处于拉直状态。由静止释放两滑块,t=3s时细绳断裂,不计滑块间的库仑力。试求:
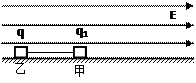
(1)细绳断裂前,两滑块的加速度。
(2)在整个运动过程中,乙的电势能增量的最大值。
(3)当乙的电势能增量为零时,甲与乙组成的系统机械能的增量。

(1)细绳断裂前,两滑块的加速度。
(2)在整个运动过程中,乙的电势能增量的最大值。
(3)当乙的电势能增量为零时,甲与乙组成的系统机械能的增量。
(1) 0.02m/s2 (2)7.2×10-7J (3)6.48×10-6J
(1)取水平向右为正方向。将甲、乙及细绳看成一个整体,根据牛顿第二定律,有
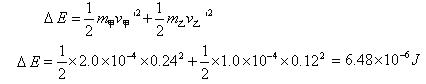

得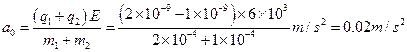
(2)当乙发生的位移最大时,乙的电势能增量最大。
细绳断裂前,甲、乙发生的位移均为
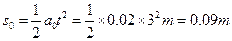
此时甲、乙的速度均为
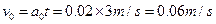
细绳断裂后,乙的加速度变为
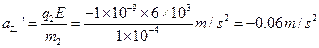
从细绳断裂到乙速度为零,乙发生的位移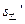 为
为
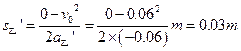
整个运动过程乙发生的最大位移为
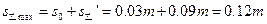
此时乙的电势能增量为
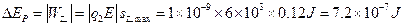
(3)当乙的总位移为零,即乙返回到原出发点时,乙的电势能增量为零。
设细绳断裂后,乙经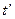 时间返回到原出发点,则有
时间返回到原出发点,则有 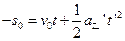
代入数据,有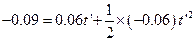
解得: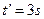
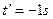 (不合题意,舍去。)
(不合题意,舍去。)
乙回到原出发点时的速度为
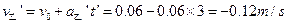
细绳断裂后,甲的加速度变为
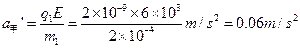
乙回到原出发点时甲的速度为
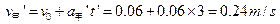
甲与乙组成的系统机械能的增量为
方法二:当乙的总位移为零,即乙返回到原出发点时,乙的电势能增量为零。此时电场力对甲所做的功即为甲与乙组成的系统机械能的增量。
设细绳断裂后,乙经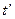 时间返回到原出发点,则有
时间返回到原出发点,则有 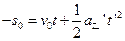
代入数据,有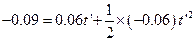
解得: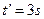
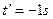 (不合题意,舍去。)
(不合题意,舍去。)
细绳断裂后,甲的加速度变为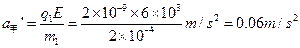
细绳断裂后,甲继续发生的位移为
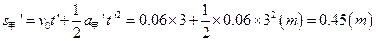
当乙的电势能增量为零时,甲发生的总位移为
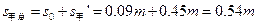
电场力对甲所做的总功为
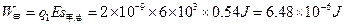
此即甲与乙组成的系统机械能的增量。
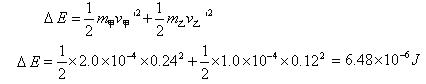

得
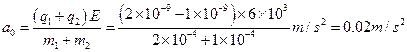
(2)当乙发生的位移最大时,乙的电势能增量最大。
细绳断裂前,甲、乙发生的位移均为
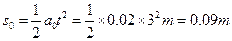
此时甲、乙的速度均为
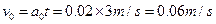
细绳断裂后,乙的加速度变为
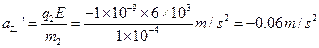
从细绳断裂到乙速度为零,乙发生的位移
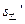 为
为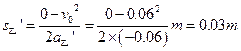
整个运动过程乙发生的最大位移为
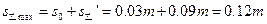
此时乙的电势能增量为
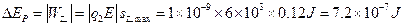
(3)当乙的总位移为零,即乙返回到原出发点时,乙的电势能增量为零。
设细绳断裂后,乙经
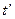 时间返回到原出发点,则有
时间返回到原出发点,则有 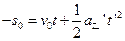
代入数据,有
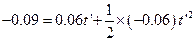
解得:
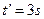
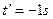 (不合题意,舍去。)
(不合题意,舍去。) 乙回到原出发点时的速度为
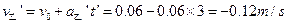
细绳断裂后,甲的加速度变为
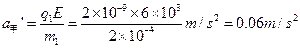
乙回到原出发点时甲的速度为
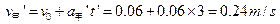
甲与乙组成的系统机械能的增量为
方法二:当乙的总位移为零,即乙返回到原出发点时,乙的电势能增量为零。此时电场力对甲所做的功即为甲与乙组成的系统机械能的增量。
设细绳断裂后,乙经
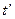 时间返回到原出发点,则有
时间返回到原出发点,则有 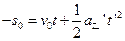
代入数据,有
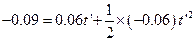
解得:
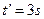
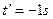 (不合题意,舍去。)
(不合题意,舍去。) 细绳断裂后,甲的加速度变为
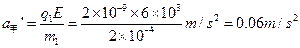
细绳断裂后,甲继续发生的位移为
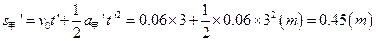
当乙的电势能增量为零时,甲发生的总位移为
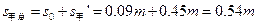
电场力对甲所做的总功为
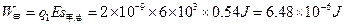
此即甲与乙组成的系统机械能的增量。

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
 电子电量为
电子电量为 )
)






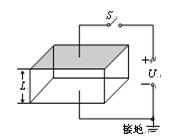
 的金属板,间距
的金属板,间距 ,当连接到
,当连接到 的高压电源正负两极时,能在两金属板间产生一个匀强电场,如图所示。现把一定量均匀分布的烟尘颗粒密闭在容器内,每立方米有烟尘颗粒
的高压电源正负两极时,能在两金属板间产生一个匀强电场,如图所示。现把一定量均匀分布的烟尘颗粒密闭在容器内,每立方米有烟尘颗粒 个,假设这些颗粒都处于静止状态,每个颗粒带电量为
个,假设这些颗粒都处于静止状态,每个颗粒带电量为 ,质量为
,质量为 ,不考虑烟尘颗粒之间的相互作用和空气阻力,并忽略烟尘颗粒所受重力。求合上电键后:
,不考虑烟尘颗粒之间的相互作用和空气阻力,并忽略烟尘颗粒所受重力。求合上电键后: