Question

【题目】有一匀强磁场分布在以为中心的一个圆形区域内，磁场方向垂直于平面（磁场未画出）。某时刻起一个质量为、电荷量为的带电粒子，由原点开始运动，初速为，方向沿轴正方向.最终粒子到达轴上的点，此时速度方向与轴的夹角为，己知的距离为，如图所示.不计重力的影响.

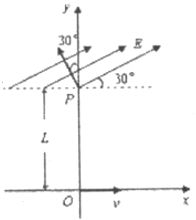
（1）求磁场区域的半径及磁场的磁感强度的大小；

（2）求带电粒子从运动到点的时间；

（3）若在点的上半部存在一与水平方向成的匀强电场，则带电粒子再次到达轴上的点点（未画出）时，距点的距离S.

Answer 1

【答案】（1）磁场区域的半径RL．磁场的磁感强度B的大小；

（2）带电粒子从O运动到P点的时间t为；

（3）若在P点的上半部存在一与水平方向成30°的匀强电场E，带电粒子再次到达y轴上的点Q点（未画出）时，距O点的距离S为L+．

【解析】

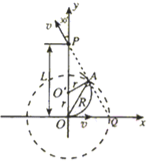
试题（1）带电粒子垂直进入磁场后，由洛伦兹力提供向心力而做匀速圆周运动，轨迹的圆心应在y轴正方向上，画出轨迹，由几何知识求出轨迹半径，由牛顿第二定律列式求出磁感强度B的大小；

（2）粒子在磁场中做匀速圆周运动，离开磁场后到P点做匀速直线运动．根据轨迹所对应的圆心角求出在磁场中运动时间，根据距离求出匀速直线运动．

（3）粒子从P点飞出后，在电场中做类平抛运动，再次到y轴时，沿电场方向与垂直电场方向的两个分位移之比等于tan30°，运用运动的分解方法，根据牛顿第二定律和运动学公式求解S．

解：（1）画出磁场区域及粒子运动的轨迹如图，设粒子圆周运动的半径为r，由几何知识可得：

r+2r=L，即得：

磁场区域的半径为

由可得：

（2）粒子做匀速圆周运动的周期为：

设粒子在磁场中运动的时间为t1，粒子在磁场中速度方向偏转120°角，则粒子轨迹所对应的圆心角为120°，则有：

粒子从A到P做匀速直线运动，设AP距离为d，所用时间为t2，则：

，

故

粒子从O到P所用时间为t，有：

（3）粒子从P点飞出后，在电场中做类平抛运动，设所用时间为t3，则：

加速度为a=

垂直于电场方向有：X=vt3

沿电场方向：Y=

又tanθ=，s=L+Xcosθ

联立上式，解得：s=L+

答：

（1）磁场区域的半径RL．磁场的磁感强度B的大小；

（2）带电粒子从O运动到P点的时间t为；

（3）若在P点的上半部存在一与水平方向成30°的匀强电场E，带电粒子再次到达y轴上的点Q点（未画出）时，距O点的距离S为L+．